
分析 利用复数代数形式的乘法运算化简,再由虚部为0求得tanθ,代入万能公式得答案.
解答 解:∵z1=4+3i,z2=cosθ+isinθ,
∴z1•z2=(4+3i)(cosθ+isinθ)=(4cosθ-3sinθ)+(3cosθ+4sinθ)i,
又z1•z2是实数,∴3cosθ+4sinθ=0,解得tanθ=$-\frac{3}{4}$,
则$\frac{1-ta{n}^{2}θ}{1+ta{n}^{2}θ}=\frac{1-(-\frac{3}{4})^{2}}{1+(-\frac{3}{4})^{2}}=\frac{7}{25}$.
故答案为:$\frac{7}{25}$.
点评 本题考查复数代数形式的乘除运算,三角函数的万能公式,是基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
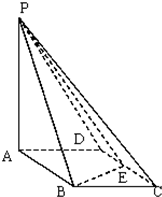 如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 年收入平均数大大增大,中位数一定变大,方差可能不变 | |
| B. | 年收入平均数大大增大,中位数可能不变,方差变大 | |
| C. | 年收入平均数大大增大,中位数可能不变,方差也不变 | |
| D. | 年收入平均数可能不变,中位数可能不变,方差可能不变 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com