
 的方程为
的方程为 ,过点
,过点 作直线与圆
作直线与圆 交于
交于 、
、 两点。
两点。
 ,求直线AB的方程;
,求直线AB的方程; 的面积最大时,求直线AB的斜率;
的面积最大时,求直线AB的斜率; 作两条直线与圆O分别交于R、S,若
作两条直线与圆O分别交于R、S,若 ,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。
,且两角均为正角,试问直线RS的斜率是否为定值,并说明理由。 ;
; 时△
时△ 面积最大,此时直线AB的斜率为
面积最大,此时直线AB的斜率为 ;
; 。
。 的直线方程为
的直线方程为 ,∵原点到直线AB的距离为
,∵原点到直线AB的距离为 ,∴
,∴ 则
则 ,∴直线AB的方程为
,∴直线AB的方程为 4′
4′ 代入圆的方程
代入圆的方程 得
得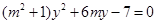

 7′
7′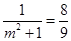 时,即
时,即 时△
时△ 面积最大,此时直线AB的斜率为
面积最大,此时直线AB的斜率为 10′
10′ ,将直线RS的方程
,将直线RS的方程 ,代入圆的方程得
,代入圆的方程得

 ①
① ,则
,则
 (*),
(*), ②
② ,即
,即 ,当
,当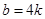 时,
时, 不成立,故直线RS的斜率为定值
不成立,故直线RS的斜率为定值 16′
16′

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com