
【题目】已知函数 ,若函数
,若函数![]() 的图象与
的图象与![]() 轴的交点个数不少于2个,则实数
轴的交点个数不少于2个,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:根据![]() 的图象与
的图象与![]() 轴的交点个数不少于2个,可得函数
轴的交点个数不少于2个,可得函数![]() 的图象与
的图象与![]() 的交点个数不少于2个,在同一坐标系中画出两个函数图象,结合图象即可得到m的取值范围.
的交点个数不少于2个,在同一坐标系中画出两个函数图象,结合图象即可得到m的取值范围.
详解:![]()
![]() 的图象与
的图象与![]() 轴的交点个数不少于2个,
轴的交点个数不少于2个,
![]() 函数
函数![]() 的图象与函数
的图象与函数![]() 的图象的交点个数不少于2个,
的图象的交点个数不少于2个,
![]() 函数
函数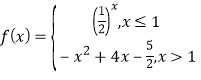 ,
,
![]()
![]() 时,函数
时,函数![]() 为指数函数,过点
为指数函数,过点![]() ,
,![]()
![]() 时,函数
时,函数![]() ,为对称轴
,为对称轴![]() ,开口向下的二次函数.
,开口向下的二次函数.
![]()
![]() ,
,
![]()
![]() 为过定点
为过定点![]() 的一条直线.
的一条直线.
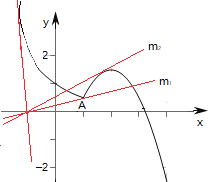
在同一坐标系中,画出两函数图象,如图所示.
(1)当![]() 时,
时,
①当![]() 过点
过点![]() 时,两函数图象有两个交点,
时,两函数图象有两个交点,
将点![]() 代入直线方程
代入直线方程![]() ,解得
,解得![]() .
.
②当![]() 与
与![]() 相切时,两函数图象有两个交点.
相切时,两函数图象有两个交点.
联立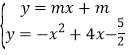 ,整理得
,整理得![]()
则![]() ,解得
,解得![]() ,
,![]() (舍)
(舍)
如图当![]() ,两函数图象的交点个数不少于2个.
,两函数图象的交点个数不少于2个.
(2)当![]() 时,易得直线
时,易得直线![]() 与函数
与函数![]() 必有一个交点
必有一个交点
如图当直线![]() 与
与![]() 相切时有另一个交点
相切时有另一个交点
设切点为![]() ,
,
![]()
![]() ,
,
![]() 切线的斜率
切线的斜率![]() , 切线方程为
, 切线方程为![]()
![]() 切线与直线
切线与直线![]() 重合,即点
重合,即点![]() 在切线上.
在切线上.
![]()
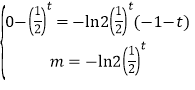 ,解得
,解得![]()
由图可知,当![]() ,两函数图象的交点个数不少于2个.
,两函数图象的交点个数不少于2个.
综上,实数![]() 的取值范围是
的取值范围是![]()
故选C.


科目:高中数学 来源: 题型:
【题目】某高校从参加今年自主招生考试的学生中随机抽取容量为![]() 的学生成绩样本,得频率分布表如下:
的学生成绩样本,得频率分布表如下:
组号 | 分组 | 频率 | 频数 |
第一组 |
|
|
|
第二组 |
| ① |
|
第三组 |
|
| ② |
第四组 |
|
|
|
第五组 |
|
|
|
合计 |
|
| |
(1)写出表中①、②位置的数据;
(2)估计成绩不低于![]() 分的学生约占多少;
分的学生约占多少;
(3)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取![]() 名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数.
名学生进行第二轮考核,分别求第三、四、五各组参加考核的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某医院中随机抽取了七位医护人员的关爱患者考核分数(患者考核:10分制),用相关的特征量![]() 表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量
表示;医护专业知识考核分数(试卷考试:100分制),用相关的特征量![]() 表示,数据如下表:
表示,数据如下表:
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程(计算结果精确到0.01);
的线性回归方程(计算结果精确到0.01);
(Ⅱ)利用(I)中的线性回归方程,分析医护专业考核分数的变化对关爱患者考核分数的影响,并估计某医护人员的医护专业知识考核分数为95分时,他的关爱患者考核分数(精确到0.1);

(Ⅲ)现要从医护专业知识考核分数95分以下的医护人员中选派2人参加组建的“九寨沟灾后医护小分队”培训,求这两人中至少有一人考核分数在90分以下的概率.
附:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
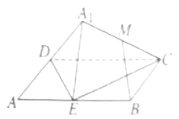
【题目】如图,在矩形![]() 中
中![]() ,E为
,E为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,
的位置,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列结论正确的是( )
的中点,则在翻折过程中,下列结论正确的是( )
A.恒有![]() 平面
平面![]()
B.B与M两点间距离恒为定值
C.三棱锥![]() 的体积的最大值为
的体积的最大值为![]()
D.存在某个位置,使得平面![]() ⊥平面
⊥平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 中点,
中点,![]() ,
,![]() .现将
.现将![]() 沿
沿![]() 折起,如图2所示,使二面角
折起,如图2所示,使二面角![]() 为
为![]() ,
,![]() 是
是![]() 的中点.
的中点.
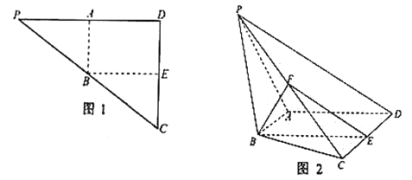
(1)求证:面![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司开设的某险种的基本保费为![]() 万元,今年参加该保险的人来年继续购买该险种的投保人称为续保人,续保人的下一年度的保费与其与本年度的出险次数的关联如下:
万元,今年参加该保险的人来年继续购买该险种的投保人称为续保人,续保人的下一年度的保费与其与本年度的出险次数的关联如下:
本年度出险次数 |
|
|
|
|
|
|
下一次保费(单位:万元) |
|
|
|
|
|
|
设今年初次参保该险种的某人准备来年继续参保该险种,且该参保人一年内出险次数的概率分布列如下:
一年内出险次数 |
|
|
|
|
|
|
概率 |
|
|
|
|
|
|
(![]() )求此续保人来年的保费高于基本保费的概率.
)求此续保人来年的保费高于基本保费的概率.
(![]() )若现如此续保人来年的保费高于基本保费,求其保费比基本保费高出
)若现如此续保人来年的保费高于基本保费,求其保费比基本保费高出![]() 的概率.
的概率.
(![]() )求该续保人来年的平均保费与基本保费的比值.
)求该续保人来年的平均保费与基本保费的比值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com