
 的定义域;
的定义域; 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源:不详 题型:解答题
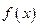 为定义在R上的偶函数,当
为定义在R上的偶函数,当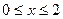 时,
时,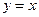 ;当
;当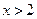 时,
时,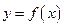 的图像时顶点在P(3,4),且过点A(2,2)的抛物线的一部分
的图像时顶点在P(3,4),且过点A(2,2)的抛物线的一部分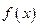 在
在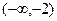 上的解析式;
上的解析式;
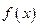 的图像;
的图像;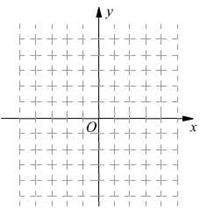
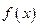 值域。
值域。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
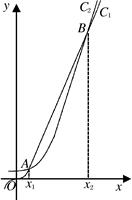
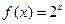 和
和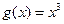 的图像的示意图如图所示, 两函数的图像在第一象限只有两个交点
的图像的示意图如图所示, 两函数的图像在第一象限只有两个交点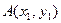 ,
,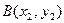 ,
,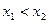
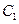 ,
,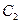 分别对应哪一个函数;(4分)
分别对应哪一个函数;(4分)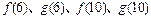 的大小,并按从小到大的顺序排列;(5分)
的大小,并按从小到大的顺序排列;(5分)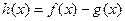 ,则函数
,则函数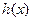 的两个零点为
的两个零点为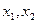 ,如果
,如果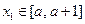 ,
,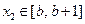 ,其中
,其中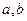 为整数,指出
为整数,指出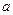 ,
,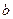 的值,并说明理由; (5分)
的值,并说明理由; (5分)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
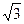 米,记∠BHE=θ.
米,记∠BHE=θ.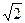 ,求此时管道的长度L;
,求此时管道的长度L;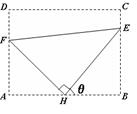
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com