考点:与二面角有关的立体几何综合题,异面直线及其所成的角
专题:综合题,空间角
分析:(1)建立空间直角坐标系.给出各点的坐标,求出
=(-1,-1,1),
=(0,1,
),利用向量的夹角公式,即可得到DM与BD
1所成角的余弦值;
(2)求出平面BCD
1、平面BC
1D
1的法向量,利用向量的夹角公式,即可求C
1-BD
1-C的大小.
解答:
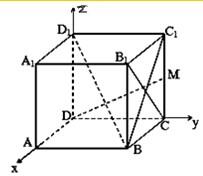
解:(1)以D为原点,DC所在的直线为y轴,DA所在的直线为x轴,DD
1所在的直线 为Z轴建立空间直角坐标系.设棱长为1,则B(1,1 0),D
1(0,0,1),D(0,0,0),M(0,1,
).
=(-1,-1,1),
=(0,1,
).
∴cos<
,
>=
=-
.
故异面直线DM与BD
1所成角的余弦值是
.
(2)C
1(0,1,1),C(0,1,0),
∴
=(-1,0,0),
=(-1,-1,1),
设平面BCD
1的法向量为
=(x,y,z),则
,∴取
=(0,1,1);
同理平面BC
1D
1的法向量为
=(1,0,-1),
∴cos<
,
>=-
,
∴<
,
>=120°,
∴二面角C
1-BD
1-C的大小为60°.
点评:本题考查异面直线DM与BD1所成角,考查二面角,考查学生分析解决问题的能力,考查向量法的运用,确定平面的法向量是关键.

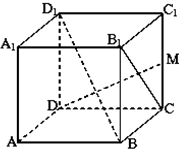 如图,正方体ABCD-A1B1C1D1中,M是CC1的中点;
如图,正方体ABCD-A1B1C1D1中,M是CC1的中点; 解:(1)以D为原点,DC所在的直线为y轴,DA所在的直线为x轴,DD1所在的直线 为Z轴建立空间直角坐标系.设棱长为1,则B(1,1 0),D1(0,0,1),D(0,0,0),M(0,1,
解:(1)以D为原点,DC所在的直线为y轴,DA所在的直线为x轴,DD1所在的直线 为Z轴建立空间直角坐标系.设棱长为1,则B(1,1 0),D1(0,0,1),D(0,0,0),M(0,1,

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案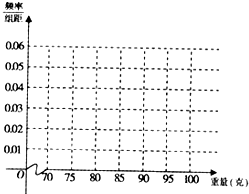 从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:
从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表: