练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列的前项和为，，且，数列满足，，对任意,都有.

    （1）求数列、的通项公式；

    （2）令.若对任意的，不等式恒成立，试求实数的取值范围.

    【答案】（1），；（2）.

    【解析】

    （1）利用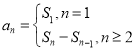，结合累乘法，求得数列的通项公式.根据已知条件判断出数列是等比数列，由此求得数列的通项公式.

    （2）利用错位相减求和法求得，利用差比较法证得是递增数列，由此求得的取值范围.化简不等式，得恒成立.构造函数，对进行分类讨论，结合二次函数的性质，求得的取值范围.

    （1）∵∴，

    当时，

    ∴，即

    ∴

    又,也满足上式，故数列的通项公式

    由，知数列是等比数列，其首项为、公比为，

    ∴数列的通项公式

    （2）∵①

    ∴②

    由①②，得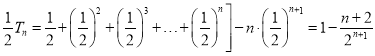

    ∴

    ∵，∴

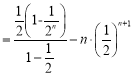
    又恒正.

    故是递增数列，

    ∴

    又.

    不等式，

    即，

    即恒成立.

    设，

    当时，恒成立，则满足条件；

    当时，由二次函数性质知不恒成立；

    当时，由于对称轴

    则在上单调递减，

    恒成立，则满足条件，

    综上所述，实数的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，以坐标原点为极点， 轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，直线的极坐标方程为，两条曲线交于两点.

    (1) 求直线与曲线交点的极坐标；

    (2) 已知为曲线 (为参数)上的一动点，设直线与曲线的交点为，求的面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知圆，圆.

    （1）若过点的直线被圆截得的弦长为，求直线的方程；

    （2）设动圆同时平分圆的周长、圆的周长.

    ①证明：动圆圆心在一条定直线上运动；

    ②动圆是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在△ABC中，已知CA=1，CB=2，∠ACB=60°．

    （1）求||；

    （2）已知点D是AB上一点，满足=λ，点E是边CB上一点，满足=λ．

    ①当λ=时，求；

    ②是否存在非零实数λ，使得⊥？若存在，求出的λ值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】中国第一高摩天轮“南昌之星摩天轮”高度为，其中心距地面，半径为，若某人从最低点处登上摩天轮，摩天轮匀速旋转，那么此人与地面的距离将随时间变化，后达到最高点，从登上摩天轮时开始计时.

    （1）求出人与地面距离与时间的函数解析式；

    （2）从登上摩天轮到旋转一周过程中，有多长时间人与地面距离大于.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列五个判断：

    ①某校高二一班和高二二班的人数分别是m，n，某次测试数学平均分分别为a，b，则这两个班的数学平均分为；

    ②10名工人生产同一种零件，生产的件数分别是15，17，14，10，15，17，17，16，14，12，设其平均数为a，中位数为b，众数为c，则有c>a>b；

    ③设m,命题“若a>b，则”的逆否命题为假命题；

    ④命题p“方程表示椭圆”，命题q“的取值范围为1<<4”，则p是q的充要条件；

    ⑤线性相关系数r越大，两个变量的线性相关性越强；反之，线性相关性越弱；

    其中正确的个数有（　 　）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）的图像上存在点，函数的图像上存在点，且关于原点对称，则的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】20名学生某次数学考试成绩(单位：分)的频率分布直方图如下：

    (1)求频率直方图中a的值；

    (2)分别求出成绩落在[50,60)与[60,70)中的学生人数；

    (3)从成绩在[50,70)的学生中人选2人，求这2人的成绩都在[60,70)中的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

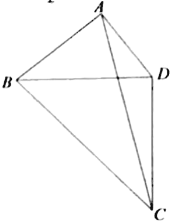
    【题目】为了美化环境，某公园欲将一块空地规划建成休闲草坪，休闲草坪的形状为如图所示的四边形ABCD．其中AB＝3百米，AD＝百米，且△BCD是以D为直角顶点的等腰直角三角形．拟修建两条小路AC，BD（路的宽度忽略不计），设∠BAD＝，(，)．

    （1）当cos＝时，求小路AC的长度；

    （2）当草坪ABCD的面积最大时，求此时小路BD的长度．

    查看答案和解析>>

    同步练习册答案