
分析 根据条件得出$\overrightarrow{a}$$•\overrightarrow{b}$=2,运用数量积的定义式得出cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$即可求出夹角,
根据向量的模与乘法的转化|$\overrightarrow{a}$+$\overrightarrow{b}$|2=($\overrightarrow{a}$$+\overrightarrow{b}$)2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2$\overrightarrow{a}•\overrightarrow{b}$,即可求解向量的模.
解答 解:∵|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,($\overrightarrow{a}$-$\overrightarrow{b}$)$⊥\overrightarrow{a}$,
∴($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,
即$\overrightarrow{a}$$•\overrightarrow{b}$=2,
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{2}{\sqrt{2}×2}=\frac{\sqrt{2}}{2}$,
即向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{4}$,
∵|$\overrightarrow{a}$+$\overrightarrow{b}$|2=($\overrightarrow{a}$$+\overrightarrow{b}$)2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2$\overrightarrow{a}•\overrightarrow{b}$=2+4+4=10
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{10}$,
故答案为:$\frac{π}{4}$;$\sqrt{10}$.
点评 本题综合考查了平面向量的性质,运算,求解夹角,模,属于基本题目,难度不大,计算仔细些,书写规范即可.


 培优口算题卡系列答案
培优口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
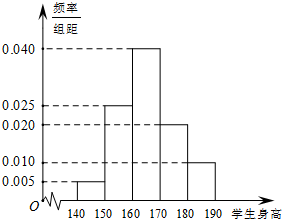 为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )
为调查学生身高的情况,随机抽测了高三两个班120名学生的身高(单位:cm),所得数据均在区间[140,190]上,其频率分布直方图如图所示(左下),则在抽测的120名学生中,身高位于区间[160,180)上的人数为( )| A. | 70 | B. | 71 | C. | 72 | D. | 73 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com