练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知向量$\overrightarrow{a}$=（2，-1），$\overrightarrow{b}$=（1，x）．
    （Ⅰ）若$\overrightarrow{a}$⊥（$\overrightarrow{a}$+$\overrightarrow{b}$），求|$\overrightarrow{b}$|的值；
    （Ⅱ）若$\overrightarrow{a}$+2$\overrightarrow{b}$=（4，-7），求向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小．

    分析 （I）由向量的加法和向量垂直的条件：数量积为0，可得x=7，再由向量的模的公式计算即可得到所求；
    （II）运用向量的加法运算，可得x=-3，再由向量的夹角公式cos＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$，计算即可得到所求夹角．

    解答 解：（I）依题意可得，$\overrightarrow{a}$+$\overrightarrow{b}$=（3，-1+x），
    由$\overrightarrow{a}$⊥（$\overrightarrow{a}$+$\overrightarrow{b}$），可得，$\overrightarrow{a}$•（$\overrightarrow{a}$+$\overrightarrow{b}$）=0，
    即6+1-x=0，
    解得x=7，即$\overrightarrow{b}$=（1，7），
    所以$|b|=\sqrt{50}=5\sqrt{2}$；
    （II）依题意$\overrightarrow{a}$+2$\overrightarrow{b}$=（4，2x-1）=（4，-7），
    可得x=-3，即$\overrightarrow{b}$=（1，-3），$\frac{2+3}{\sqrt{5}•\sqrt{10}}$
    所以cos＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{2+3}{\sqrt{5}•\sqrt{10}}$=$\frac{\sqrt{2}}{2}$，
    因为＜$\overrightarrow{a}$，$\overrightarrow{b}$＞∈[0，π]，
    所以$\overrightarrow{a}$与$\overrightarrow{b}$的夹角大小是$\frac{π}{4}$．

    点评 本题考查向量的数量积的运算，主要考查向量的模的求法和夹角的求法，考查运算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．△ABC的三角形A，B，C所对三边分别是a，b，c，B=60°，cosC=$\frac{4}{5}$，b=$\sqrt{3}$，则sinA=$\frac{3+4\sqrt{3}}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．Sn是数列{an}的前n项和，且a1=1，an+1=2an+n-1，S10=1991．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．设数列{an}的前n项和为Sn，且a1=-1，an+1=Sn•Sn+1，则数列{an}的通项公式an=$\left\{\begin{array}{l}{-1，n=1}\\{\frac{1}{n（n-1）}，n≥2}\end{array}\right.$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

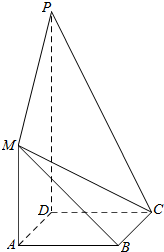    4．如图，正方形ABCD与梯形AMPD所在的平面互相垂直，AD⊥PD，MA∥PD，MA=AD=$\frac{1}{2}$PD=1．
    （Ⅰ）求证：MB∥平面PDC；
    （Ⅱ）求二面角M-PC-D的余弦值；
    （Ⅲ）E为线段PC上一点，若直线DE与直线PM所成的角为60°，求PE的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

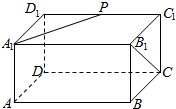    14．如图，在长方体ABCD-A1B1C1D1中，设 AD=AA1=1，AB=2，P是C1D1的中点，则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°，$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．给定函数①y=x${\;}^{\frac{1}{2}}$②y=log${\;}_{\frac{1}{2}}$（x+1）③y=|x2-2x|④y=（$\frac{5}{6}$）x，其中在区间（0，1）上单调递减的函数序号是（　　）
    A．①④B．②④C．②③D．①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知α∈（0，$\frac{π}{2}$），且cos（α+$\frac{π}{3}$）=-$\frac{3}{5}$，则sinα的值为（　　）
    A．$\frac{3-4\sqrt{3}}{10}$B．$\frac{3+4\sqrt{3}}{10}$C．$\frac{4-3\sqrt{3}}{10}$D．$\frac{4+3\sqrt{3}}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．设向量$\overrightarrow{a}$=（1，4cosx），$\overrightarrow{b}$=（4$\sqrt{3}$sinx，1），x∈R．
    （1）若x∈（$\frac{π}{2}$，π），且|$\overrightarrow{a}$|=$\sqrt{2}$，求sin（x+$\frac{π}{4}$），cos2x，tan2x的值；
    （2）设函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$，求f（x）在[0，π]上的值域．

    查看答案和解析>>

    同步练习册答案