
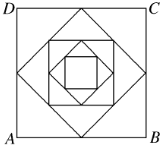
 如图,正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,问爬行2n条线段的长度的平方和是多少?
如图,正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,问爬行2n条线段的长度的平方和是多少?
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 4 |
| ||
| 2 |
| a2 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| a2 |
| 4 |
1-(
| ||
1-
|
| a2 |
| 2 |
| 1 |
| 4 |


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 逻辑思维能力 运动协调能力 |
一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | b | 1 |
| 优秀 | 1 | 3 | a |
| 3 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
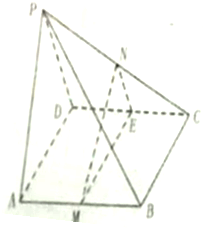 在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.
在四棱锥P-ABCD中,ABCD是矩形,PA⊥平面ABCD,M、N、E分别是AB、PC、CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com