Question

14．（1）在边长为1的正方形ABCD内任取一点M，求事件“|AM|≤1”的概率；
（2）某班在一次数学活动中，老师让全班56名同学每人随机写下一对都小于1的正实数x、y，统计出两数能与1构成锐角三角形的三边长的数对（x，y）共有12对，请据此估计π的近似值（精确到0.001）．

Answer 1

分析 （1）根据已知条件，求出满足条件的正方形ABCD的面积，及事件“|AM|≤1”对应平面区域的面积，代入几何概型计算公式，即可求出答案．
（2）以点A为坐标原点，AB为x轴，AD为y轴建立平面直角坐标系，如图所示：任取两个小于1的正数x，y，所有基本事件构成区域$Ω=\left\{{（x，y）|\left\{\begin{array}{l}0＜x＜1\\ 0＜y＜1\end{array}\right.}\right\}$，即正方形ABCD内部；事件N=“以x，y与1为边长能构成锐角三角形”包含的基本事件构成区域$N=\left\{{（x，y）|\left\{\begin{array}{l}0＜x＜1\\ 0＜y＜1\\ x+y＞1\\{x^2}+{y^2}＞1\end{array}\right.}\right\}$，即扇形BAD以外正方形ABCD以内的阴影部分，由几何概型概率计算公式，得出所取的点在圆内的概率是圆的面积比正方形的面积，二者相等即可估计π的值．

解答 解：（1）如图，在边长为1的正方形ABCD内任取一点M，满足条件的点M落在扇形BAD内（图中阴影部分），由几何概型概率计算公式，有：$P（|MA|≤1）=\frac{{{S_{阴影部分}}}}{{{S_{正方形ABCD}}}}=\frac{π}{4}$，
故事件“|AM|≤1”发生的概率为$\frac{π}{4}$．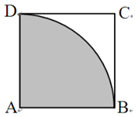

（2）以点A为坐标原点，AB为x轴，AD为y轴建立平面直角坐标系，如图所示：任取两个小于1的正数x，y，所有基本事件构成区域$Ω=\left\{{（x，y）|\left\{\begin{array}{l}0＜x＜1\\ 0＜y＜1\end{array}\right.}\right\}$，即正方形ABCD内部；
事件N=“以x，y与1为边长能构成锐角三角形”包含的基本事件构成区域$N=\left\{{（x，y）|\left\{\begin{array}{l}0＜x＜1\\ 0＜y＜1\\ x+y＞1\\{x^2}+{y^2}＞1\end{array}\right.}\right\}$，即扇形BAD以外正方形ABCD以内的阴影部分；
由（1）知：$P（N）=1-\frac{π}{4}$，
全班56名同学每人随机写下一对都小于1的正实数x、y，可以看作在区域Ω中任取56个点；满足“以x，y与1为边长能构成锐角三角形”的（x，y）共有12对，即有12个点落在区域N中，
故其概率为$\frac{12}{56}=\frac{3}{14}$，用频率估计概率，有$1-\frac{π}{4}≈\frac{3}{14}$，即$\frac{π}{4}≈\frac{11}{14}$，
∴$π≈\frac{11}{14}×4=\frac{22}{7}≈3.143$，即π的近似值为3.143．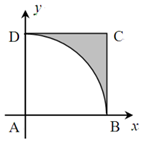

点评 本题考查了随机模拟法求圆周率的问题，也考查了几何概率的应用问题，几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．