
 某幼儿园小班的美术课上,老师带领小朋友们用水彩笔为美术本上如右图所示的两个大小不同的气球涂色,要求一个气球只涂一种颜色,两个气球分别涂不同的颜色.该班的小朋友牛牛现可用的有暖色系水彩笔红色、橙色各一支,冷色系水彩笔绿色,蓝色,紫色各一支.
某幼儿园小班的美术课上,老师带领小朋友们用水彩笔为美术本上如右图所示的两个大小不同的气球涂色,要求一个气球只涂一种颜色,两个气球分别涂不同的颜色.该班的小朋友牛牛现可用的有暖色系水彩笔红色、橙色各一支,冷色系水彩笔绿色,蓝色,紫色各一支.| 红色 | 橙色 | 绿色 | 蓝色 | 紫色 | |
| 红色 | 0 | 1 | 1 | 1 | 1 |
| 橙色 | 1 | 0 | 1 | 1 | 1 |
| 绿色 | 1 | 1 | 0 | 2 | 2 |
| 蓝色 | 1 | 1 | 2 | 0 | 2 |
| 紫色 | 1 | 1 | 2 | 2 | 0 |
| 6 |
| 20 |
| 3 |
| 10 |
|
|
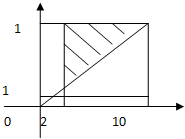 (10分)
(10分)| 1 |
| 2 |
| 32 |
| 72 |
| 4 |
| 9 |


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 2 |
sin(4π-α)cos(3π+α)cos(
| ||||
cos(π-α)sin(3π-α)sin(-π-α)sin(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com