
分析 (Ⅰ)由题得c=1,$\frac{2{b}^{2}}{a}$=$\sqrt{2}$,a2=2,b2=1,即可求椭圆的方程;
(Ⅱ)把直线方程和椭圆方程联立,求出关于A,B两点坐标和直线斜率之间的关系,再代入$\overrightarrow{OA}$•$\overrightarrow{OB}$的表达式即可求出求$\overrightarrow{OA}$•$\overrightarrow{OB}$的范围;
(Ⅲ)先把直线方程和椭圆方程联立,求出关于A,B两点坐标和直线斜率之间的关系,求出$\overrightarrow{OA}$+$\overrightarrow{OB}$,利用向量$\overrightarrow{a}$=(-2$\sqrt{2}$,1)与$\overrightarrow{OA}$+$\overrightarrow{OB}$共线,求出直线斜率.
解答 解:(Ⅰ)由题得c=1,$\frac{2{b}^{2}}{a}$=$\sqrt{2}$,∴a2=2,b2=1,
所以椭圆的方程是$\frac{{x}^{2}}{2}+{y}^{2}$=1;
(Ⅱ)当k存在时,设直线方程为y=k(x-1).
联立$\frac{{x}^{2}}{2}+{y}^{2}$=1,化简为(2k2+1)x2-4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),x1+x2=$\frac{4{k}^{2}}{2{k}^{2}+1}$,x1x2=$\frac{2{k}^{2}-2}{2{k}^{2}+1}$.
$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=$\frac{{k}^{2}-2}{2{k}^{2}+1}$.
令$\frac{{k}^{2}-2}{2{k}^{2}+1}$=m,则${k}^{2}=\frac{m+2}{1-2m}$≥0,
∴-2≤m<$\frac{1}{2}$,∴-2≤$\overrightarrow{OA}$•$\overrightarrow{OB}$<$\frac{1}{2}$,
当k不存在时,A(1,$\frac{\sqrt{2}}{2}$),B(1,-$\frac{\sqrt{2}}{2}$),则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{1}{2}$,
综上,-2≤$\overrightarrow{OA}$•$\overrightarrow{OB}$≤$\frac{1}{2}$,
(Ⅲ)$\overrightarrow{OA}$+$\overrightarrow{OB}$=(x1+x2,y1+y2),
∵向量$\overrightarrow{a}$=(-2$\sqrt{2}$,1)与$\overrightarrow{OA}$+$\overrightarrow{OB}$共线,
∴-2$\sqrt{2}$(y1+y2)=x1+x2,
∴-2$\sqrt{2}$[k(x1-1)+k(x2-1)]=x1+x2,
由韦达定理知k=0或k=$\sqrt{2}$.
点评 本题综合考查了直线与椭圆的位置关系以及向量共线问题.直线与圆锥曲线的位置关系,由于集中交汇了直线,圆锥曲线两章的知识内容,综合性强,能力要求高,还涉及到函数,方程,不等式,平面几何等许多知识,可以有效的考查函数与方程的思想,数形结合的思想,分类讨论的思想和转化化归的思想,因此,这一部分内容也成了高考的热点和重点.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
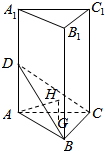 如图所示,三棱柱ABC-A1B1C1的底面是正三角形,侧棱AA1⊥底面ABC,AB=1,AA1=2,点D在侧棱AA1上,点G,H分别是△ABC,△BCD的重心.
如图所示,三棱柱ABC-A1B1C1的底面是正三角形,侧棱AA1⊥底面ABC,AB=1,AA1=2,点D在侧棱AA1上,点G,H分别是△ABC,△BCD的重心.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com