
| �װ� | �Ұ� | �ϼ� | |
| ���� | 14 | 8 | 22 |
| ������ | 6 | 12 | 18 |
| �ϼ� | 20 | 20 | 40 |
| P��x2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.79 | 10.828 |
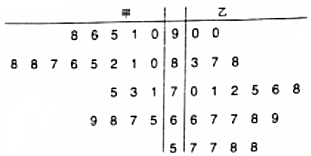
���� ��1��������Ұ���ѧ�ɼ�������80���������ɼ�Ϊ90�ֵ�ͬѧ�������������������û����¼��ĸ��������ùŵ���͵ĸ��ʹ�ʽ���㣻
��2�����ݾ�Ҷͼ�ֱ�����ס��Ұ�����������벻������������г����������������ָ����ʽ����K2�Ĺ۲�ֵ���Ƚ����ٽ�ֵ�Ĵ�С���жϳɼ��������ѧ��ʽ�йصĿɿ��Գ̶ȣ�
��� �⣺��1���Ұ���ѧ�ɼ�������80�ֵ�ͬѧ��5�������гɼ�Ϊ90�ֵ�ͬѧ��2����
��5��ͬѧ�г�ȡ2��������C52=10�ַ�����
����������һ��ͬѧ90�ֵij鷨��C22+C21C31=7�֣�
���������P=$\frac{7}{10}$��
��2��2��2��������
| �װ� | �Ұ� | �ϼ� | |
| ���� | 14 | 8 | 22 |
| ������ | 6 | 12 | 18 |
| �ϼ� | 20 | 20 | 40 |
���� ���⿼�����ɾ�Ҷͼ�������������������������������������ָ��K2�Ĺ۲�ֵ�������˹ŵ���͵ĸ��ʼ��㣬�ۺ���ǿ������Ҫϸ�ģ��ɹ�ʽ�������ָ��K2�Ĺ۲�ֵ���ɹ۲�ֵ�жϳɼ��������ѧ��ʽ�йصĿɿ��Գ̶��ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\frac{{\sqrt{2}}}{2}��1��$ | B�� | $��0��\frac{{\sqrt{2}}}{2}��$ | C�� | $��\frac{{\sqrt{3}}}{2}��1��$ | D�� | $��0��\frac{{\sqrt{3}}}{2}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -9 | B�� | 9 | C�� | 6 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | an=n | B�� | an=n2 | C�� | an=$\frac{n}{2}$ | D�� | an=$\frac{{n}^{2}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{3}$ | B�� | $\frac{��}{6}$ | C�� | $\frac{��}{3}$��$\frac{2��}{3}$ | D�� | $\frac{��}{6}$��$\frac{5��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\sqrt{2}-1$ | D�� | $2-\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{2}$ | B�� | 2 | C�� | $\frac{3}{2}$ | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com