
| A、[-3,0) | ||||
B、[-3,-
| ||||
C、[-3,-
| ||||
D、(-
|


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x) |
| ex |
| A、f(2)>e2g(0),f(2014>e2014g(0) |
| B、f(2)>e2g(0),f(2014)<e2014g(0) |
| C、f(2)<e2g(0),f(2014)<e2014g(0) |
| D、f(2)<e2g(0),g(2014)>e2014g(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| log3an |
| an |
| A、先单增,再单减 |
| B、单调递减 |
| C、单调递增 |
| D、先单减,再单增 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,不规则图形ABCD中:AB和CD是线段,AD和BC是圆弧,直线l⊥AB于E,当l从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设AE=x,左侧部分面积为y,则y关于x的大致图象为( )
如图,不规则图形ABCD中:AB和CD是线段,AD和BC是圆弧,直线l⊥AB于E,当l从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设AE=x,左侧部分面积为y,则y关于x的大致图象为( )A、 |
B、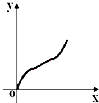 |
C、 |
D、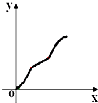 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com