
���� ��1��ͨ������������{bn-an}����2Ϊ���$-\frac{1}{2}$Ϊ���ȵĵȱ����У������ɵý��ۣ�
��2��ͨ�����οɵ�${a_n}_{+1}+{b_{n+1}}-8=\frac{1}{2}��{a_n}+{b_n}-8��$��ȡn=1���ý��ۣ�
��3��ͨ��an+bn=8��${b_n}-{a_n}=2•{��-\frac{1}{2}��^{n-1}}$��ʽ��ӿɵ�Sn=4n+$\frac{2}{3}$[1-��-$\frac{1}{2}$��n]��ͨ��p•��Sn-4n����[1��3]������ɵ�$\frac{1}{1-��-\frac{1}{2}��^{n}}$��$\frac{2p}{3}$��$\frac{3}{1-��-\frac{1}{2}��^{n}}$����n����ż�����ۣ��ɵ�$\frac{1}{1-��-\frac{1}{2}��^{n}}$�����ֵΪ$\frac{4}{3}$��$\frac{3}{1-��-\frac{1}{2}��^{n}}$����СֵΪ2�������ɵý��ۣ�
��� �⣺��1��${b_{n+1}}-{a_n}_{+1}=\frac{{4+{a_n}}}{2}-\frac{{4+{b_n}}}{2}=\frac{{{a_n}-{b_n}}}{2}=-\frac{1}{2}��{b_n}-{a_n}��$��
��b1-a1=2����{bn-an}����2Ϊ���$-\frac{1}{2}$Ϊ���ȵĵȱ����У�
��${b_n}-{a_n}=2•{��-\frac{1}{2}��^{n-1}}$��
��2����${a_n}_{+1}+{b_{n+1}}=\frac{{4+{b_n}}}{2}+\frac{{4+{a_n}}}{2}=\frac{{{a_n}+{b_n}}}{2}+4$��
��${a_n}_{+1}+{b_{n+1}}-8=\frac{1}{2}��{a_n}+{b_n}-8��$��
��a1+b1-8=0����an+bn-8=0�������
��an+bn=8Ϊ��ֵ��
��3���ɣ�1����2���ã�an+bn=8��${b_n}-{a_n}=2•{��-\frac{1}{2}��^{n-1}}$��
��ʽ��Ӽ��ã�${b_n}=4+{��-\frac{1}{2}��^{n-1}}$��
��Sn=4n+$\frac{1-��-\frac{1}{2}��^{n}}{1-��-\frac{1}{2}��}$=4n+$\frac{2}{3}$[1-��-$\frac{1}{2}$��n]��
��p•��Sn-4n��=$\frac{2p}{3}$•[1-��-$\frac{1}{2}$��n]��
��p•��Sn-4n����[1��3]����1��$\frac{2p}{3}$•[1-��-$\frac{1}{2}$��n]��3��
��1-��-$\frac{1}{2}$��n��0����$\frac{1}{1-��-\frac{1}{2}��^{n}}$��$\frac{2p}{3}$��$\frac{3}{1-��-\frac{1}{2}��^{n}}$��
��nΪ����ʱ��$\frac{1}{1-��-\frac{1}{2}��^{n}}$=$\frac{1}{1+\frac{1}{{2}^{n}}}$��n���������������0��$\frac{1}{1-��-\frac{1}{2}��^{n}}$��1��
��nΪż��ʱ��$\frac{1}{1-��-\frac{1}{2}��^{n}}$=$\frac{1}{1-\frac{1}{{2}^{n}}}$��n���������������$\frac{1}{1-��-\frac{1}{2}��^{n}}$��1��
��$\frac{1}{1-��-\frac{1}{2}��^{n}}$�����ֵΪ$\frac{4}{3}$��$\frac{3}{1-��-\frac{1}{2}��^{n}}$����СֵΪ2��
��$\frac{1}{1-��-\frac{1}{2}��^{n}}$��$\frac{2p}{3}$��$\frac{3}{1-��-\frac{1}{2}��^{n}}$��
��$\frac{4}{3}$��$\frac{2p}{3}$��2����ã�2��p��3��
��ʵ��p��ȡֵ��ΧΪ��[2��3]��
���� ���⿼�������е�ͨ�����������۵�˼�룬�����������������ע����ⷽ���Ļ��ۣ������е��⣮


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
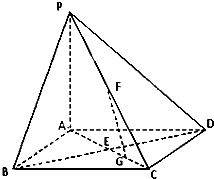 ��ͼ���ڵ����������ε�����P-ABCD�У�PA����ABCD��BD��AC�ڵ�E��F��PC�е㣬GΪAC��һ�㣮
��ͼ���ڵ����������ε�����P-ABCD�У�PA����ABCD��BD��AC�ڵ�E��F��PC�е㣬GΪAC��һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{3\sqrt{2}}}{4}$ | B�� | -$\frac{{\sqrt{2}}}{4}$ | C�� | -$\frac{{3\sqrt{2}}}{4}$ | D�� | $\frac{{\sqrt{2}}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5��k��-4 | B�� | -4��k��-3 | C�� | -5��k��-3 | D�� | k=-4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com