
| A�� | -5��k��-4 | B�� | -4��k��-3 | C�� | -5��k��-3 | D�� | k=-4 |
���� ��c5=a5����b6��a5��a5��b5��b6��a5���ɴ��Ƶ���-5��k��-4����c5=b5����b5��a5��b5��a5��a4��b5���ɴ��Ƶ���-5��k��-3���ɴ������ʵ��k��ȡֵ��Χ
��� �⣺��c5=a5����a5��b5����ǰ�治����bn���
��{bn}������{an}�ݼ�����bi��i=1��2��3��4����b5��a5��ai��i=1��2��3��4����
��an�ݼ����൱n��6ʱ������cn��an����cn=bn��
��ʱӦ��b6��a5����a5��b5����20��5+k����k��-4��
b6��a5����6+k��1����k��-5��
��-5��k��-4��
��c5=b5����b5��a5��ͬ����ǰ�治����bn�
��a4��b5��b4����n��6ʱ����{bn}������{an}�ݼ���
��bn��b5��a5��an��n��6����
�൱n��6ʱ��cn=bn����b5��a5����5+k��1���ã�k��-4��
��a4��b5����2��5+k����k��-3����-4��k��-3��
���ϵã�-5��k��-3��
��ʵ��k��ȡֵ��Χ��[-5��-3]��
��ѡ��C
���� ���⿼��ʵ����ȡֵ��Χ�����ۺ���ǿ���Ѷȴ���ʱҪ�������յȲ����к͵ȱ����е����ʵ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ʱ��x/Сʱ | 2 | 3 | 5 | 8 | 9 | 12 |
| ����y/Ԫ | 30 | 40 | 60 | 90 | 120 | m |
| A�� | 125Ԫ | B�� | 128Ԫ | C�� | 140Ԫ | D�� | 142.7Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ���е�����������ͼ����������������עˮ��������ˮ��ĸ߶���ʱ��仯�Ŀ���ͼ���ǣ�������
��ͼ��һ���е�����������ͼ����������������עˮ��������ˮ��ĸ߶���ʱ��仯�Ŀ���ͼ���ǣ�������| A�� | 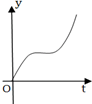 | B�� |  | C�� | 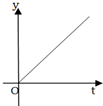 | D�� | 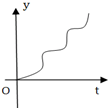 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 22014-1 | B�� | 22015-1 | C�� | 22015+1 | D�� | 22016-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com