
分析 ①运用诱导公式证明sin(x+π)=-sin(x)=sin(-x);
②根据奇函数,周期性定义得出f(x+2)=f(-x)=-f(x),f(x+4)=f(x);
③根据解析式得出f(x+4)=f(-x),f(x)关于x=2对称,即f(2-x)=f(2+x),f(x)为偶函数,根题意得出图象也关于点(-1,0)成中心对称,
且在(-2,-1)上单调递减,利用偶函数的对称得出:在(1,2)上单调递增;
④利用定义式对称f(x)=f(-x),f(x+3)=f(-x)=f(x),推论得出f(x)为偶函数,且周期为3;
解答 解:①∵sin(x+π)=-sin(x)=sin(-x),
∴函数y=sinx具有“P(a)性质”;
∴①正确
②∵若奇函数y=f(x)具有“P(2)性质”,
∴f(x+2)=f(-x)=-f(x),
∴f(x+4)=f(x),
周期为4,
∵f(1)=1,f(2015)=f(3)=-f(1)=-1,
∴②不正确,
③∵若函数y=f(x)具有“P(4)性质”,
∴f(x+4)=f(-x),
∴f(x)关于x=2对称,
即f(2-x)=f(2+x),
∵图象关于点(1,0)成中心对称,
∴f(2-x)=-f(x),
即f(2+x)=-f(-x),
∴得出:f(x)=f(-x),
f(x)为偶函数,
∵图象关于点(1,0)成中心对称,且在(-1,0)上单调递减,
∴图象也关于点(-1,0)成中心对称,且在(-2,-1)上单调递减,
根据偶函数的对称得出:在(1,2)上单调递增;
故③正确.
④∵“P(0)性质”和“P(3)性质”,
∴f(x)=f(-x),f(x+3)=f(-x)=f(x),
∴f(x)为偶函数,且周期为3,
所以对$?{x_1},{x_2}∈[{-\frac{1}{2},\frac{5}{2}}]$,为一个周期,都有|f(x1)-f(x2)|≥2成立,
则则?x1,x2∈R,都有|f(x1)-f(x2)|≥2成立,故④正确.
故答案为:①③④
点评 本题考查了新概念的题目,函数的对称周期性,主要运用抽象函数性质判断,难度较大,特别是第3个选项,仔细推证.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:填空题
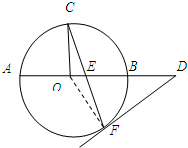 如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.
如图,AB是⊙O的直径,C,F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连结CF交AB于点E,OA=3,DB=3,则DE=3$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
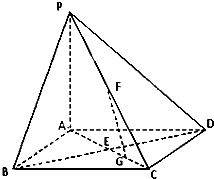 如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
如图,在底面是正方形的四棱锥P-ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | -$\frac{{\sqrt{2}}}{4}$ | C. | -$\frac{{3\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5≤k≤-4 | B. | -4≤k≤-3 | C. | -5≤k≤-3 | D. | k=-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com