
 如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )
如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是( )| A. | 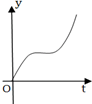 | B. |  | C. | 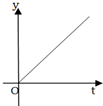 | D. | 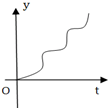 |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
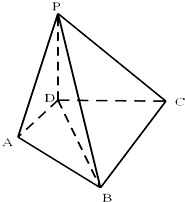 如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5≤k≤-4 | B. | -4≤k≤-3 | C. | -5≤k≤-3 | D. | k=-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
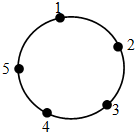 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(0)<f(\frac{3}{5})<f(-\frac{1}{2})$ | B. | $f(0)<f(-\frac{1}{2})<f(\frac{3}{5})$ | C. | $f(\frac{3}{5})<f(-\frac{1}{2})<f(0)$ | D. | $f(-\frac{1}{2})<f(0)<f(\frac{3}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
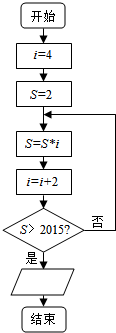
| A. | 输出i-2 | B. | 输出i-1 | C. | 输出i | D. | 输出i+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com