
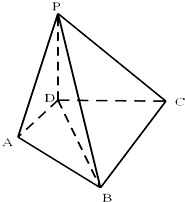
 如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.分析 (Ⅰ)首先求出平面PDC的垂线,找到PB与平面PDC所成角的平面角;
(Ⅱ)由已知得到平面PDB⊥平面ABCD,作CH⊥BD于H,则CH⊥平面PDB,作HF⊥PB于F,连CF,得到∠CFH为二面角D-PB-C的平面角,然后通过解三角形求之;
(Ⅲ)取PB中点G,PC中点E,连结AG,GE,DE,得到四边形AGED是平行四边形,只要得到AG⊥平面PBC,利用面面垂直的判定定理证明.
解答 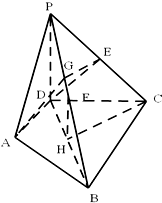 解:(Ⅰ)∵PD⊥平面ABCD
解:(Ⅰ)∵PD⊥平面ABCD
∴PD⊥BC,
由AD⊥DC,AD∥BC,得BC⊥DC,
又PD∩DC=D,则BC⊥平面PDC,
∴∠BPC为直线PB与平面PDC所成的角,
令PD=1,则DC=1,BC=$\sqrt{2}$,得PC=$\sqrt{2}$,
由BC⊥平面PDC
∴BC⊥PC,
在Rt△PBC中,由PC=BC得∠BPC=45°即直线PB和面PDC所成的角为45°;
(Ⅱ)由PD⊥平面ABCD,PD?平面PDB,得平面PDB⊥平面ABCD,
作CH⊥BD于H,则CH⊥平面PDB,作HF⊥PB于F,连CF,
∴CF⊥PB
则∠CFH为二面角D-PB-C的平面角,
在Rt△DBC中,DB=$\sqrt{B{C}^{2}+C{D}^{2}}=\sqrt{3}$,
∴CH•BD=CD•BC,得CH=$\frac{\sqrt{6}}{3}$,
在Rt△FHC中,得HF=$\frac{\sqrt{3}}{3}$
∴tan∠HFC=$\frac{HC}{HF}=\sqrt{2}$
即二面角D-PB-C的正切值为$\sqrt{2}$;
(Ⅲ)证明:取PB中点G,PC中点E,连结AG,GE,DE
∴GE∥BC,GE=$\frac{1}{2}$BC,由已知∴AD∥BC,AD=$\frac{1}{2}$BC,
∴AD=GE,AD∥GE,则四边形AGED是平行四边形,
∴AG∥DE,可知DE⊥平面PBC,
∴AG⊥平面PBC,
又AG?平面PAB
∴平面PAB⊥平面PBC.
点评 本题考查了线面垂直面面垂直的性质定理和判定定理的运用以及二面角的求法;关键是转化为平面角解答.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | [-2,1] | B. | (2,+∞) | C. | (1,2) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | $\frac{16}{3}$ | D. | ±3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 时间x/小时 | 2 | 3 | 5 | 8 | 9 | 12 |
| 工资y/元 | 30 | 40 | 60 | 90 | 120 | m |
| A. | 125元 | B. | 128元 | C. | 140元 | D. | 142.7元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com