
分析 (1)由a1=1,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$.两边取倒数可得:$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,利用等差数列的定义即可证明;
(2)由(1)可得:$\frac{1}{{a}_{n}}$=2n-1,可得:anan+1=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,利用“裂项求和”与“放缩法”即可得出.
解答 (1)证明:∵a1=1,an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$.
两边取倒数可得:$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=2,
∴数列{$\frac{1}{{a}_{n}}$}是等差数列,首项为1,公差为2;
(2)解:由(1)可得:$\frac{1}{{a}_{n}}$=1+2(n-1)=2n-1,
∴an=$\frac{1}{2n-1}$.
∴anan+1=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴Sn=a1a2+a2a3+…+anan+1=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})]$=$\frac{1}{2}(1-\frac{1}{2n+1})$,
∴2Sn=1-$\frac{1}{2n+1}$<1,
即2Sn<1.
点评 本题考查了等差数列的定义、“裂项求和”与“放缩法”,考查了推力能力与计算能力,属于中档题.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).
如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
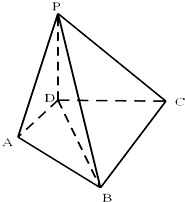 如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
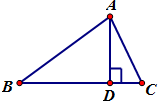 如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )
如图,在△ABC中,AB=2,∠ABC=θ,AD是边BC上的高,当θ∈[$\frac{π}{6}$,$\frac{π}{3}$]时,$\overrightarrow{AD}$•$\overrightarrow{AC}$的最大值与最小值之差为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
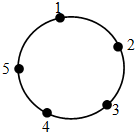 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点,若它停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从5这个点开始跳,则经2015次跳后停在的点对应的数为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com