
分析 设F(c,0)的直线为$\left\{\begin{array}{l}{x=c+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),代入椭圆方程,运用韦达定理,注意参数的几何意义,可将上面中的c换成$\frac{{a}^{2}}{c}$,化简整理结合离心率公式,即可得证.
解答 证明:设F(c,0)的直线为$\left\{\begin{array}{l}{x=c+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),
代入椭圆方程可得,(b2cos2α+a2sin2α)t2+2b2ctcosα+b2c2-b2a2=0,
则t1t2=$\frac{{b}^{2}{c}^{2}-{b}^{2}{a}^{2}}{{b}^{2}co{s}^{2}α+{a}^{2}si{n}^{2}α}$=-$\frac{{b}^{4}}{{b}^{2}co{s}^{2}α+{a}^{2}si{n}^{2}α}$,
即有|$\overrightarrow{FM}$|•|$\overrightarrow{FN}$|=$\frac{{b}^{4}}{{b}^{2}co{s}^{2}α+{a}^{2}si{n}^{2}α}$,
由于过A与直线MN平行的直线交椭圆于B、C两点,
可将上面中的c换成$\frac{{a}^{2}}{c}$,即有
|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|=$\frac{{b}^{2}•\frac{{a}^{4}}{{c}^{2}}-{b}^{2}{a}^{2}}{{b}^{2}co{s}^{2}α+{a}^{2}si{n}^{2}α}$=$\frac{{a}^{2}}{{c}^{2}}$•(-$\frac{{b}^{2}{c}^{2}-{b}^{2}{a}^{2}}{{b}^{2}co{s}^{2}α+{a}^{2}si{n}^{2}α}$)=$\frac{1}{{e}^{2}}$•$\frac{{b}^{4}}{{b}^{2}co{s}^{2}α+{a}^{2}si{n}^{2}α}$,
故有|$\overrightarrow{FM}$|•|$\overrightarrow{FN}$|=e2|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|.
点评 本题考查直线和椭圆的位置关系,考查联立直线的参数方程和椭圆方程,运用韦达定理和离心率公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (0,1] | C. | [3,+∞) | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
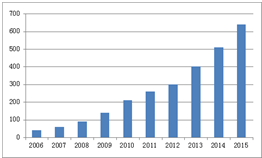 某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )
某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=ax3+b | D. | y=alnx+b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com