
分析 留言函数的奇偶性求出b,然后判断l1斜率存在,且不为0.设l1的斜率为k,则l1的斜率为-$\frac{1}{k}$,则l1的方程为y+2=k(x-1),l2的方程为y+2=-$\frac{1}{k}$(x-1).若直线l1和l2,它们与二次函数y=ax2(a>0)的图象都没有公共点,则他们的方程与抛物线方程联立所得的方程无解,进而得到满足条件的a的取值范围.
解答 解:函数f(x)=ax2+bx+c的值域为[0,+∞),且f(-x)=f(x),x∈R,
可得b=0,c=0;a>0,
二次函数化为y=ax2(a>0)
易知l1斜率存在,且不为0.设l1的斜率为k,则l1的斜率为-$\frac{1}{k}$,
则l1的方程为y+2=k(x-1),l2的方程为y+2=-$\frac{1}{k}$(x-1).
由$\left\{\begin{array}{l}y={ax}^{2}\\ y+2=k(x-1)\end{array}\right.$得,ax2-kx+k+2=0.
由l1与二次函数y=ax2(a>0)的图象没有公共点知,△1=k2-4a(k+2)<0…①.
同理,由l2与二次函数y=ax2(a>0)的图象没有公共点知,△2=(-$\frac{1}{k}$)2-4a(-$\frac{1}{k}$+2)<0…②.
由①得2a-2$\sqrt{{a}^{2}+2a}$<k<2a+2$\sqrt{{a}^{2}+2a}$;
由②得k<$\frac{a-\sqrt{{a}^{2}+2a}}{4a}$,或k>$\frac{a+\sqrt{{a}^{2}+2a}}{4a}$.
依题意,方程组①②有解.
∵若方程组①②无解?2a-2$\frac{a-\sqrt{{a}^{2}+2a}}{4a}$≥$\frac{a-\sqrt{{a}^{2}+2a}}{4a}$且2a+2$\sqrt{{a}^{2}+2a}$≤$\frac{a+\sqrt{{a}^{2}+2a}}{4a}$,即0<a≤$\frac{1}{8}$.
∴方程组①②有解⇒a>$\frac{1}{8}$.
故a的取值范围为($\frac{1}{8}$,+∞).
故答案为:($\frac{1}{8}$,+∞).
点评 本题考查的知识点是函数的奇偶性,二次函数的最值,二次函数的性质,其中将直线与抛物线没有交点,转化为联立所得的方程组无解,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | y=cos2x | B. | y=sin2x | C. | y=|cosx| | D. | y=|sinx| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
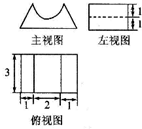
| A. | 27-$\frac{3π}{2}$ | B. | 18-$\frac{3π}{2}$ | C. | 27-3π | D. | 18-3π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).
如图,在几何体ABCDN中,CD⊥平面ABC,DC∥AN,CD=2AN=4,又AB=AC=BC=2,点P是BD上的动点(与B、D两点不重合).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
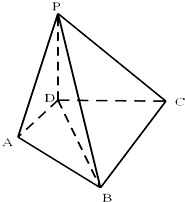 如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图所示,PD⊥平面ABCD,AD⊥CD,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com