
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 取AB中点G,推导出∠GEF是异面直线EF与AC所成的角(或所成角的补角),由此能求出异面直线EF与AC所成的角的大小.
解答 解: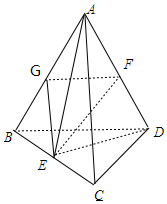 取AB中点G,连结AE、DE、GE、GF,
取AB中点G,连结AE、DE、GE、GF,
则AE=DE=$\sqrt{{a}^{2}-\frac{{a}^{2}}{4}}$=$\frac{\sqrt{3}}{2}a$,EF=$\sqrt{(\frac{\sqrt{3}}{2}a)^{2}-(\frac{a}{2})^{2}}$=$\frac{\sqrt{2}}{2}a$,
GF=GE=$\frac{a}{2}$,GE∥AC,
∴∠GEF是异面直线EF与AC所成的角(或所成角的补角),
∴cos∠GEF=$\frac{\frac{{a}^{2}}{4}+\frac{2}{4}{a}^{2}-\frac{{a}^{2}}{4}}{2×\frac{a}{2}×\frac{\sqrt{2}}{2}a}$=$\frac{\sqrt{2}}{2}$,
∴∠GEF=45°.
∴异面直线EF与AC所成的角为45°.
故选:B.
点评 本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
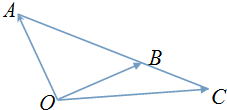
| A. | $\overrightarrow{c}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\frac{3}{2}$$\overrightarrow{b}$ | B. | $\overrightarrow{c}$=$\frac{3}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\overrightarrow{c}$=-$\overrightarrow{a}$+2$\overrightarrow{b}$ | D. | $\overrightarrow{c}$=$\overrightarrow{a}$+2$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 4 | D. | 非上述情况 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 36 | C. | 42 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com