
分析 (1)求出函数的导数,由导数的几何意义得f′(2)=1,解得即可;
(2)求出函数的导数,令导数大于0,得增区间,令导数小于0,得减区间,注意x>0;
(3)根据函数的单调性与导数的关系可得g'(x)≤0在[1,2]上恒成立,即-$\frac{2}{{x}^{2}}$+2x+$\frac{2a}{x}$≤0在[1,2]上恒成立.即a≤$\frac{1}{x}$-x2在[1,2]上恒成立.利用导数求出函数h(x)=$\frac{1}{x}$-x2在[1,2]上的最小值,即可得出结论.
解答 解:(1)函数f(x)=x2+2alnx的导数为f′(x)=2x+$\frac{2a}{x}$,
由已知f'(2)=1,即4+a=1,解得a=-3.
(2)f(x)=x2-6lnx的导数为f′(x)=2x-$\frac{6}{x}$,x>0.
由f′(x)>0,可得x>$\sqrt{3}$,f′(x)<0,可得0<x<$\sqrt{3}$,
即有f(x)的减区间为(0,$\sqrt{3}$),增区间为($\sqrt{3}$,+∞);
(3)由g(x)=$\frac{2}{x}$+x2+2alnx,得g′(x)=-$\frac{2}{{x}^{2}}$+2x+$\frac{2a}{x}$,
由已知函数g(x)为[1,2]上的单调减函数,
则g'(x)≤0在[1,2]上恒成立,
即-$\frac{2}{{x}^{2}}$+2x+$\frac{2a}{x}$≤0在[1,2]上恒成立.
即a≤$\frac{1}{x}$-x2在[1,2]上恒成立.
令h(x)=$\frac{1}{x}$-x2,在[1,2]上h′(x)=-$\frac{1}{{x}^{2}}$-2x<0,
所以h(x)在[1,2]为减函数.h(x)min=h(2)=-$\frac{7}{2}$,
所以a≤-$\frac{7}{2}$.
点评 本题主要考查导数的几何意义,利用导数研究函数的单调性、最值等知识,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | $t>\frac{4}{75}$ | B. | $\frac{8}{75}<t≤\frac{3}{25}$ | C. | $\frac{4}{75}<t<\frac{3}{50}$ | D. | $\frac{4}{75}<t≤\frac{3}{50}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线x2=4y的焦点为F,过焦点F且不平行于x轴的动直线l交抛物线于A(x1,y1),B(x2,y2)两点,抛物线在A、B两点处的切线交于点M.
已知抛物线x2=4y的焦点为F,过焦点F且不平行于x轴的动直线l交抛物线于A(x1,y1),B(x2,y2)两点,抛物线在A、B两点处的切线交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -$\frac{1}{4}$ | C. | -$\frac{1}{4}$或-4 | D. | -$\frac{1}{4}$或4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=30°,则∠PCE等于( )
如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE,BE,∠APE的平分线分别与AE、BE相交于C、D,若∠AEB=30°,则∠PCE等于( )| A. | 150° | B. | 75° | C. | 105° | D. | 60° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图:平面上两点P(0,1),Q(3,6),在直线y=x上取两点M,N,使$|MN|=\sqrt{2}$且使|PM|+|MN|+|NQ|的值取最小,则N的坐标为$(\frac{9}{4},\frac{9}{4})$.
如图:平面上两点P(0,1),Q(3,6),在直线y=x上取两点M,N,使$|MN|=\sqrt{2}$且使|PM|+|MN|+|NQ|的值取最小,则N的坐标为$(\frac{9}{4},\frac{9}{4})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
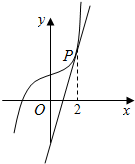 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com