
分析 (1)两次点数之和为16,即两次的底面数字为:(1,3),(2,2),(3,1),可得P(A).
(2)X的可能取值为0,1,2,3,利用相互独立与古典概率计算公式即可得出.
解答 解:(1)两次点数之和为16,即两次的底面数字为:(1,3),(2,2),(3,1),
P(A)=$\frac{3}{4×4}$=$\frac{3}{16}$.…(5分)
(2)X的可能取值为0,1,2,3
且P(X=0)=$\frac{4}{4×4}$=$\frac{1}{4}$,P(X=1)=$\frac{3×2}{4×4}$=$\frac{3}{8}$,P(X=2)=$\frac{2×2}{4×4}$=$\frac{1}{4}$,P(X=3)=$\frac{2}{4×4}$=$\frac{1}{8}$.…(9分)
则X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{4}$ | $\frac{3}{8}$ | $\frac{1}{4}$ | $\frac{1}{8}$ |
点评 本题考查了相互独立与古典概率计算公式、随机变量分布列的性质及其数学期望,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
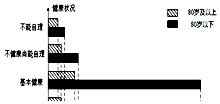 我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:
我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了解老人们的健康状况,政府从 老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能 自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行 统计,样本分布被制作成如图表:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 4 | D. | $\frac{68}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{π}{2})>2f(\frac{π}{6})$ | B. | $\sqrt{3}f(\frac{π}{4})>\sqrt{2}f(\frac{π}{3})$ | C. | $\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$ | D. | $f(1)<2f(\frac{π}{6})sin1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2017 | C. | 2016 | D. | 4034 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 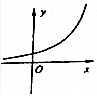 | B. | 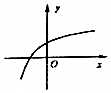 | C. | 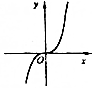 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com