
分析 (1)每次能飞出的概率为$\frac{1}{3}$,利用相互独立事件的概率公式可求笨鸟第四次能飞出窗户的概率;
(2)用ξ表示聪明鸟试飞的次数,则ξ=1,2,3,则P(ξ=k)=$\frac{1}{3}$,可求;
(3)用η表示笨鸟试飞的次数,则P(η<ξ)=P(η=1,ξ=2)+P(η=1,ξ=3)+P(η=2,ξ=3)可求.
解答 解:(1)笨鸟第四次能飞出窗户的概率P=$\frac{2}{3}×\frac{2}{3}×\frac{2}{3}×\frac{1}{3}$=$\frac{8}{81}$.(4分)
(2)用ξ表示聪明鸟试飞的次数,则ξ=1,2,3.
则P(ξ=1)=$\frac{1}{3}$,P(ξ=2)=$\frac{2}{3}×\frac{1}{2}=\frac{1}{3}$,P(=3)=$\frac{2}{3}×\frac{1}{2}×1$=$\frac{1}{3}$
分布列为P(ξ=k)=$\frac{1}{3}$(ξ=1,2.3)(8分)
(3)用η表示笨鸟试飞的次数,
则P(η<ξ)=P(η=1,ξ=2)+P(η=1,ξ=3)+P(η=2,ξ=3)
=$\frac{1}{3}×\frac{1}{3}+\frac{1}{3}×\frac{1}{3}+(\frac{2}{3}×\frac{1}{3})×\frac{1}{3}$=$\frac{8}{27}$(12分)
点评 本题主要考查了离散型简单随机变量的分布列的求解,属于基础试题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 若α⊥β,m∥α,则m⊥β | B. | 若m∥α,n∥m,则n∥α | ||
| C. | 若m∥α,n∥β,且m∥n,则α∥β | D. | 若m⊥β,m∥α,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )
设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )| A. | f(-1) | B. | f(-2) | C. | f(1) | D. | f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
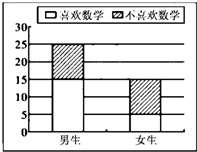 对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.
对某中学高二某班40名学生是否喜欢数学课程进行问卷调查,将调查所得数据绘制成二堆条形图如图所示.| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 | 40 |
| P(K2≥k0) | 0.5 | 0.4 | 0.25 | 0.15 | 0.1 | 0.01 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com