
| A. | 点(π,0)是函数y=f(x)图象的一个对称中心 | |
| B. | 直线x=$\frac{π}{2}$是函数y=f(x)图象的一条对称轴 | |
| C. | π是函数y=f(x)的周期 | |
| D. | 函数y=f(x)的最大值为1 |
分析 对于A选项,用中心对称的充要条件,直接验证f(2π-x)+f(x)=0是否成立即可判断其正误;
对于B选项,用轴对称的条件直接验证f(π-x)=f(x)成立与否即可判断其正误;
对于C选项,用周期函数的定义直接验证f(x+π)=f(x)成立与否即可判断其正误;
对于D选项,利用三角函数的性质即可直接判断.
解答 解:A、∵f(2π-x)+f(x)=sin(2π-x)cos2(2π-x)+sinxcos2x=-sinxcos2x+sinxcos2x=0,∴点(π,0)是函数y=f(x)图象的一个对称中心,故A正确;
B、∵f(π-x)=sin(π-x)cos2(π-x)=sinxcos2x=f(x),∴f(x)关于直线x=$\frac{π}{2}$对称,故B正确;
C、∵f(x+π)=sin(π+x)cos2(π+x)=-sinxcos2x=-f(x),∴π不是函数y=f(x)的周期,故C错误;
D、∵sinx∈[-1,1],cos2x∈[-1,1],可得f(x)=sinxcos2x的最大值为1,故D正确.
故选:C.
点评 本题考查三角函数的对称性,考查了三角函数值域的解法,考查排除法在选择题中的应用,属于中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
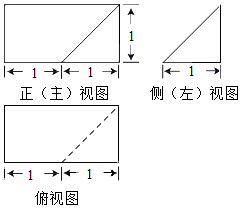
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
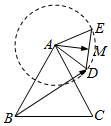 如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )
如图,等边△ABC的边长为2,△ADE也是等边三角形且边长为1,M为DE的中心,在△ABC所在平面内,△ADE绕A逆时针旋转一周,$\overrightarrow{BD}$•$\overrightarrow{AM}$的最大值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{4}$+$\sqrt{3}$ | C. | $\frac{3+\sqrt{3}}{4}$ | D. | $\frac{3}{4}$+2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {a|0≤a<1} | B. | {a|-1<a≤0} | C. | {a|-1<a<1} | D. | {a|a∈R,a∉Z} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com