解答:
解:设P(x
0,y
0)是函数g(x)=|log
2|x-1||的图象上任一点,
则当x=2-x
0时,y=|log
2|(2-x
0)-1||=|log
2|x
0-1||=y
0∴点Q(2-x
0,y
0)也在函数g(x)=|log
2|x-1||的图象上.
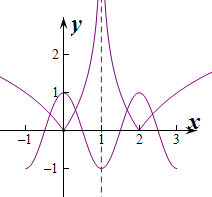
由于点P、Q关于直线x=1对称,
∴函数g(x)=|log
2|x-1||的图象关于直线x=1对称.
当x=1时,函数f(x)=cos(πx)=cosπ=-1
∴函数f(x)=cos(πx)的图象关于直线x=1对称.
∴函数f(x)=cos(πx)与函数g(x)=|log
2|x-1||的图象的交点关于直线x=1对称.
当1<x<2时,函数f(x)=cos(πx)单调递增,f(1)=-1,f(2)=1;
而函数g(x)=|log
2|x-1||=-log
2(x-1)单调递减,g(2)=0,
故在区间(1,2)内,函数f(x)=cos(πx)与函数g(x)=|log
2|x-1||的图象有且只一个交点;
当2≤x≤3时,函数f(x)=cos(πx)单调递减,f(2)=1,f(3)=-1,
而函数g(x)=|log
2|x-1||=log
2(x-1)单调递增,g(2)=0,
故在区间(2,3)内,函数f(x)=cos(πx)与函数g(x)=|log
2|x-1||的图象有且只一个交点;
当x>3时,g(x)=|log
2|x-1||=log
2(x-1)>1,而函数f(x)=cos(πx)≤1,
故在区间(3,+∞)内,函数f(x)=cos(πx)与函数g(x)=|log
2|x-1||的图象无交点.
综上所述,函数f(x)=cos(πx)与函数g(x)=|log
2|x-1||的图象共有4个交点,关于直线x=1对称,
∴函数f(x)=cos(πx)与函数g(x)=|log
2|x-1||的图象所有交点的横坐标之和为4.




 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案