
分析 (Ⅰ)由题意得log2(x-1)≥0,从而解出集合A,再化简集合B,从而求交集;
(Ⅱ)结合(I)知C={x|m-6≤x≤4m},B=[1,16],且B⊆C;从而可得$\left\{\begin{array}{l}{m-6≤1}\\{4m≥16}\end{array}\right.$,从而解得.
解答 解:(Ⅰ)由题意得,log2(x-1)≥0,
故x≥2;
故A=[2,+∞),
∵-4≤x≤0,
∴1≤($\frac{1}{2}$)x≤16,
故B=[1,16],
故A∩B=[2,16];
(Ⅱ)∵C={x|m-6≤x≤4m},B=[1,16],且B⊆C,
∴$\left\{\begin{array}{l}{m-6≤1}\\{4m≥16}\end{array}\right.$,
解得,4≤m≤7.
点评 本题考查了函数的定义域与值域的求法及集合的运算与集合关系的应用,属于基础题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.
如图,在△ABC中,|$\overrightarrow{AB}$|=4,|$\overrightarrow{AC}$|=2,∠BAC=90°,D,E,F分别是边BC,CA,AB上的点且$\overrightarrow{CE}$=$\frac{1}{4}\overrightarrow{CA}$,$\overrightarrow{AF}$=$\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{BD}$=$\frac{1}{4}\overrightarrow{BC}$,则$\overrightarrow{DE}$•$\overrightarrow{DF}$的值为$\frac{11}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{1{2}^{2}}$=1 | B. | $\frac{{x}^{2}}{1{3}^{2}}$-$\frac{{y}^{2}}{{5}^{2}}$=1 | ||
| C. | $\frac{{x}^{2}}{{3}^{2}}$-$\frac{{y}^{2}}{{4}^{2}}$=1 | D. | $\frac{{x}^{2}}{{4}^{2}}$-$\frac{{y}^{2}}{{3}^{2}}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
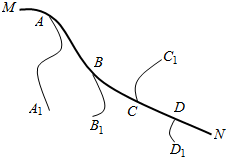
| A. | A处 | B. | D处 | ||
| C. | B、C间的任何一处(包括B、C) | D. | A、B之间的任何一处(包括A、B) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | C. | 向左平移2个单位 | D. | 向右平移2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25% | B. | 20% | C. | 30% | D. | 50% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
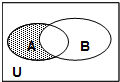 已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )
已知全集U=R,集合A={x|x>1},集合B={x|3x-4≤0},满足如图所示的阴影部分的集合是( )| A. | {x|x>1} | B. | {x|1<x≤$\frac{4}{3}$} | C. | {x|x≤1} | D. | {x|x>$\frac{4}{3}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com