练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．定义在 R 上的奇函数 f （x） 满足 f （2+x ）=f （2-x），且 f （1）=1，则 f （2017）=（　　）
    A．0B．1C．-1D．-2

    分析 求出函数的周期，然后利用周期性以及函数的奇偶性求解即可．

    解答 解：定义在R上的奇函数f（x）满足 f （2+x ）=f （2-x），且 f （1）=1，
    可得f（x+4）=f（-x）=-f（x），f（x+8）=f（x），T=8，
    f（2017）=f（1）=1．
    故选B．

    点评 本题考查函数的奇偶性以及函数的周期性的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    19．函数$y=sin（2x+\frac{π}{3}）$的图象经过下列平移，可以得到函数$y=cos（2x+\frac{π}{6}）$图象的是（　　）
    A．向右平移$\frac{π}{6}$个单位B．向左平移$\frac{π}{6}$个单位
    C．向右平移$\frac{π}{3}$个单位D．向左平移$\frac{π}{3}$个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知$\overline{z}$为复数z的共轭复数，且（1-i）z=1+i，则$\overline{z}$为（　　）
    A．-iB．iC．1-iD．1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知 x＞1，y＞1，且 lg x，$\frac{1}{4}$，lg y 成等比数列，则 xy 有（　　）
    A．最小值10B．最小值$\sqrt{10}$C．最大值10D．最大值  $\sqrt{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知λ∈R，向量$\overrightarrow{a}$=（ 3，λ ），$\overrightarrow{b}$=（λ-1，2），则“λ=$\frac{3}{5}$”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

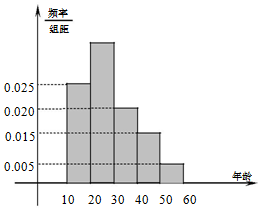    14．•滑雪场开业当天共有 500 人滑雪，滑雪服务中心根据他们的年龄分成[10，20），[20，30），[30，40），[40，50），[50，60]五个组，现按照分层抽样的方法选取 20 人参加有奖活动，这些人的样本数据的频率分布直方图如下图所示，从左往右分别为一组、二组、三组、四组、五组．
    （Ⅰ）求开业当天所有滑雪的人年龄在[20，30）有多少人？
    （Ⅱ）在选取的这 20 人样本中，从年龄不低于 30 岁的人中任选两人参加抽奖活动，求这两个人来自同一组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知点M（0，$\sqrt{15}$）及抛物线y2=4x上一动点N（x，y），则x+|MN|的最小值为（　　）
    A．$\sqrt{5}$B．$2\sqrt{3}$C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．经过原点且到点A（1，1）的距离是$\sqrt{2}$的直线方程为x+y=0．．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．交强险是车主必须为机动车购买的险种．若普通6座以下私家车投保交强险第一年的费用（基准保费）统一为a元，在下一年续保时，实行的是费率浮动机制，保费与上一年度车辆发生道路交通事故的情况相联系，发生交通事故的次数越多，费率也就越高，具体浮动情况如表：
     交强险浮动因素和浮动费率比率表
      浮动因素浮动比率 
     A1 上一个年度未发生有责任道路交通事故 下浮10%
     A2 上两个年度未发生有责任道路交通事故 下浮20%
     A3 上三个及以上年度未发生有责任道路交通事故 下浮30%
     A4 上一个年度发生一次有责任不涉及死亡的道路交通事故 0%
     A5 上一个年度发生两次及两次以上有责任道路交通事故 上浮10%
     A6 上一个年度发生有责任道路交通死亡事故 上浮30%
    某机构为了研究某一品牌普通6座以下私家车的投保情况，随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况，统计得到了下面的表格：
     类型 A1 A2 A3 A4 A5 A6
     数量10 5 5 20 15 5 
    以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率，完成下列问题：
    （Ⅰ）按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定a=950．记X为某同学家的一辆该品牌车在第四年续保时的费用，求X的分布列与数学期望值；（数学期望值保留到个位数字）
    （Ⅱ）某二手车销售商专门销售这一品牌的二手车，且将下一年的交强险保费高于基本保费的车辆记为事故车．假设购进一辆事故车亏损5000元，一辆非事故车盈利10000元：
    ①若该销售商购进三辆（车龄已满三年）该品牌二手车，求这三辆车中至多有一辆事故车的概率；
    ②若该销售商一次购进100辆（车龄已满三年）该品牌二手车，求他获得利润的期望值．

    查看答案和解析>>

    同步练习册答案