
分析 非零数a,b满足3a=2b(a+1),则$\frac{1}{2b}$=$\frac{a+1}{3a}$,代入直线方程,整理可得(6x+y)+a(y-3)=0.令y-3=0,则6x+y=0,即可得出结论.
解答 解:∵非零数a,b满足3a=2b(a+1),
∴$\frac{1}{2b}$=$\frac{a+1}{3a}$,
∵$\frac{2x}{a}$+$\frac{y}{2b}$=1
∴$\frac{2x}{a}$+$\frac{a+1}{3a}$•y=1,
∴6x+(a+1)y=3a,
∴(6x+y)+a(y-3)=0.
令y-3=0,则6x+y=0,∴x=-$\frac{1}{2}$,y=3,
∴定点坐标为(-$\frac{1}{2}$,3).
故答案为:(-$\frac{1}{2}$,3).
点评 本题考查直线恒过定点,考查学生的计算能力,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
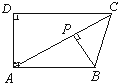 如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )
如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )| A. | AB与AD | B. | AB与BC | C. | BD与BC | D. | AD与AP |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
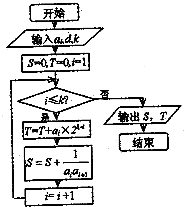 如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)
如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{π}{3}$] | B. | [$\frac{π}{3}$,$\frac{π}{2}$) | C. | [$\frac{π}{6}$,$\frac{π}{3}$] | D. | ($\frac{π}{4}$,$\frac{π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{7}^{4}$ | B. | C${\;}_{8}^{4}$ | C. | C${\;}_{8}^{3}$ | D. | C${\;}_{9}^{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com