
| A. | (-∞,0) | B. | (0,2) | C. | (2,+∞) | D. | (-∞,0)∪(2,+∞) |
分析 设出直线AF的方程,与抛物线联立,求出B的坐标,求出直线AB,FN的斜率,从而求出直线BN的方程,根据A、M、N三点共线,可求出M的横坐标的表达式,从而求出m的取值范围.
解答 解:抛物线方程为y2=4x,F(1,0),可设A(t2,2t),t≠0,t≠±1,
∵AF不垂直y轴,
∴设直线AF:x=sy+1(s≠0),
联立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=sy+1}\end{array}\right.$,得y2-4sy-4=0.
y1y2=-4,
∴B($\frac{1}{{t}^{2}}$,-$\frac{2}{t}$),
又直线AB的斜率为$\frac{2t}{{t}^{2}-1}$,故直线FN的斜率为$\frac{{t}^{2}-1}{2t}$,
从而得FN:y=-$\frac{{t}^{2}-1}{2t}$(x-1),直线BN:y=-$\frac{2}{t}$,
则N($\frac{{t}^{2}+3}{{t}^{2}-1}$,-$\frac{2}{t}$),
设M(m,0),由A、M、N三点共线,得$\frac{2t}{{t}^{2}-m}$=$\frac{2t+\frac{2}{t}}{{t}^{2}-\frac{{t}^{2}+3}{{t}^{2}-1}}$,
于是m=$\frac{2{t}^{2}}{{t}^{2}-1}$=$\frac{2}{1-\frac{1}{{t}^{2}}}$,得m<0或m>2.
经检验,m<0或m>2满足题意.
∴点M的横坐标的取值范围为(-∞,0)∪(2,+∞).
故选D.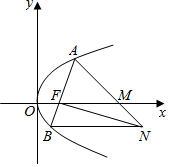
点评 本题考查抛物线的简单性质,考查直线与圆锥曲线位置关系的应用,考查数学转化思想方法,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{5π}{12}$个单位 | B. | 向右平移$\frac{5π}{12}$个单位 | ||
| C. | 向左平移$\frac{7π}{12}$个单位 | D. | 向右平移$\frac{7π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某大型超市拟对店庆当天购物满288元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.
某大型超市拟对店庆当天购物满288元的顾客进行回馈奖励.规定:顾客转动十二等分且质地均匀的圆形转盘(如图),待转盘停止转动时,若指针指向扇形区域,则顾客可领取此区域对应面额(单位:元)的超市代金券.假设转盘每次转动的结果互不影响.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )
如图所示,已知二面角α-l-β的平面角为θ,PA⊥α,PB⊥β,A、B为垂足,且PA=4,PB=5,设A、B到棱l的距离分别为x、y,当θ变化时,点(x,y)的轨迹是下列图形中的( )| A. |  | B. |  | C. | 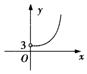 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直三棱柱ABC-A1B1C1的所有棱长都相等,D,E分别是AB,A1C1的中点,如图所示.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,D,E分别是AB,A1C1的中点,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com