
【题目】某精密仪器生产厂准备购买![]() ,
,![]() ,
,![]() 三种型号数控车床各一台,已知这三台车床均使用同一种易损件.在购进机器时,可以额外购买这种易损件作为备件,每个0.1万元.在机器使用期间,如果备件不足再购买,则每个0.2万元.现需要决策在购买机器时应同时购买几个易损件,为此搜集并整理了三种型号各120台车床在一年使用期内更换的易损零件数,得到如下统计表:
三种型号数控车床各一台,已知这三台车床均使用同一种易损件.在购进机器时,可以额外购买这种易损件作为备件,每个0.1万元.在机器使用期间,如果备件不足再购买,则每个0.2万元.现需要决策在购买机器时应同时购买几个易损件,为此搜集并整理了三种型号各120台车床在一年使用期内更换的易损零件数,得到如下统计表:
每台车床在一年中更换易损件的件数 | 5 | 6 | 7 | |
频数 |
| 60 | 60 | 0 |
| 30 | 60 | 30 | |
| 0 | 80 | 40 | |
将调查的每种型号车床在一年中更换的易损件的频率视为概率,每台车床在易损件的更换上相互独立.
(Ⅰ)求一年中![]() ,
,![]() ,
,![]() 三种型号车床更换易损件的总数超过18件的概率;
三种型号车床更换易损件的总数超过18件的概率;
(Ⅱ)以一年购买易损件所需总费用的数学期望为决策依据,问精密仪器生产厂在购买车床的同时应购买18件还是19件易损件?
【答案】(Ⅰ)![]() ;(Ⅱ)时应当购买18件易损件.
;(Ⅱ)时应当购买18件易损件.
【解析】
(Ⅰ)由频数表可得三种型号更换的易损件的概率,设一年中![]() 、
、![]() 、
、![]() 三种型号车床更换易损件分别为
三种型号车床更换易损件分别为![]() ,
,![]() ,
,![]() ,三种型号车床更换易损件的总数为
,三种型号车床更换易损件的总数为![]() ,利用相互独立事件的概率分别求出
,利用相互独立事件的概率分别求出![]() 和
和![]() ,由
,由![]() ,从而得解;
,从而得解;
(Ⅱ)由题可知,![]() 的可能取值为16,17,18,19,20,由对立事件的概率可知
的可能取值为16,17,18,19,20,由对立事件的概率可知![]() ,由(Ⅰ)可知
,由(Ⅰ)可知![]() 和
和![]() ,从而可得关于
,从而可得关于![]() 的分布列,然后分别求出购买18件和19件易损件的总费用的数学期望,比较大小后作出判断即可.
的分布列,然后分别求出购买18件和19件易损件的总费用的数学期望,比较大小后作出判断即可.
解:(Ⅰ)由表中数据可得三种型号更换的易损件的概率(频率)分布表为:
每台车床在一年中更换易损件的件数 | 5 | 6 | 7 | |
概率(频率) |
|
|
| 0 |
|
|
|
| |
| 0 |
|
| |
设一年中![]() ,
,![]() ,
,![]() 三种型号车床更换易损件分别为
三种型号车床更换易损件分别为![]() ,
,![]() ,
,![]() ,
,
三种型号车床更换易损件的总数为![]() ,
,
![]()
![]() ,
,
![]() ,
,
所以![]() ,
,
所以一年中![]() ,
,![]() ,
,![]() 三种型号车床更换易损件的总数超过18件的概率为
三种型号车床更换易损件的总数超过18件的概率为![]() .
.
(Ⅱ)由题意,![]() 所有可能取值为16,17,18,19,20,
所有可能取值为16,17,18,19,20,
由(Ⅰ)可知![]() ,
,
故![]() 的概率分布列为:
的概率分布列为:
|
| 19 | 20 |
|
|
|
|
设购买18件的总费用为![]() ,则
,则![]() 的可能取值为1.8,2,2.2,
的可能取值为1.8,2,2.2,
则![]() 万元,
万元,
设购买19件的总费用为![]() ,则
,则![]() 的可能取值为1.9,2.1,
的可能取值为1.9,2.1,
则![]() 万元,
万元,
![]() ,所以在购买车床的同时应当购买18件易损件.
,所以在购买车床的同时应当购买18件易损件.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 、
、![]() 两点分别是椭圆
两点分别是椭圆![]() 的上、下顶点,
的上、下顶点,![]() 是等腰直角三角形,延长
是等腰直角三角形,延长![]() 交椭圆
交椭圆![]() 于
于![]() 点,且
点,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 、
、![]() 的动点,直线
的动点,直线![]() 、
、![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 、
、![]() 两点,点
两点,点![]() ,试问:
,试问:![]() 外接圆是否恒过
外接圆是否恒过![]() 轴上的定点(异于点
轴上的定点(异于点![]() )?若是,求该定点坐标;若否,说明理由.
)?若是,求该定点坐标;若否,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是我国大陆地区从2013年至2019年国内生产总值(GDP)近似值(单位:万亿元人民币)的数据表格:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
中国大陆地区GDP: (单位:万亿元人民币) |
|
|
|
|
|
|
|
![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(Ⅱ)党的十九大报告中指出:从2020年到2035年,在全面建成小康社会的基础上,再奋斗15年,基本实视社会主义现代化.若到2035年底我国人口增长为![]() 亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
亿人,假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示.
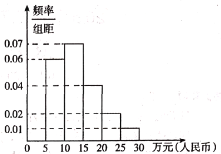
以(Ⅰ)的结论为依据,预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值.
参考数据:![]() ,
,![]() .
.
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: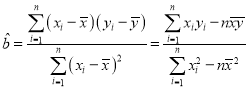 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省![]() 年开始将全面实施新高考方案.在
年开始将全面实施新高考方案.在![]() 门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为
门选择性考试科目中,物理、历史这两门科目采用原始分计分;思想政治、地理、化学、生物这4门科目采用等级转换赋分,将每科考生的原始分从高到低划分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共
共![]() 个等级,各等级人数所占比例分别为
个等级,各等级人数所占比例分别为![]() 、
、![]() 、
、![]() 、
、![]() 和
和![]() ,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
,并按给定的公式进行转换赋分.该省组织了一次高一年级统一考试,并对思想政治、地理、化学、生物这4门科目的原始分进行了等级转换赋分.
(1)某校生物学科获得![]() 等级的共有10名学生,其原始分及转换分如下表:
等级的共有10名学生,其原始分及转换分如下表:
原始分 | 91 | 90 | 89 | 88 | 87 | 85 | 83 | 82 |
转换分 | 100 | 99 | 97 | 95 | 94 | 91 | 88 | 86 |
人数 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 1 |
现从这10名学生中随机抽取3人,设这3人中生物转换分不低于![]() 分的人数为
分的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)假设该省此次高一学生生物学科原始分![]() 服从正态分布
服从正态分布![]() .若
.若![]() ,令
,令![]() ,则
,则![]() ,请解决下列问题:
,请解决下列问题:
①若以此次高一学生生物学科原始分![]() 等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
等级的最低分为实施分层教学的划线分,试估计该划线分大约为多少分?(结果保留为整数)
②现随机抽取了该省![]() 名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记
名高一学生的此次生物学科的原始分,若这些学生的原始分相互独立,记![]() 为被抽到的原始分不低于
为被抽到的原始分不低于![]() 分的学生人数,求
分的学生人数,求![]() 取得最大值时
取得最大值时![]() 的值.
的值.
附:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,四边形
,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 交于点
交于点![]() ,
, ![]() 是
是![]() 上任意一点.
上任意一点.
(1)求证: ![]() ;
;
(2)已知二面角![]() 的余弦值为
的余弦值为![]() ,若
,若![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
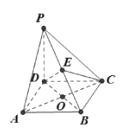
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知真命题:“函数![]() 的图象关于点
的图象关于点![]() 成中心对称图形”的充要条件为“函数
成中心对称图形”的充要条件为“函数![]() 是奇函数”.
是奇函数”.
(Ⅰ)将函数![]() 的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数
的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(Ⅱ)求函数![]() 图象对称中心的坐标;
图象对称中心的坐标;
(Ⅲ)已知命题:“函数![]() 的图象关于某直线成轴对称图象”的充要条件为“存在实数
的图象关于某直线成轴对称图象”的充要条件为“存在实数![]() 和
和![]() ,使得函数
,使得函数![]() 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节,一场突如其来的新型冠状病毒感染的肺炎疫情,牵动着我们每个人的心,严重扰乱了大家的正常生活,在全国人民的共同努力下,疫情得到了有效的控制.已知某市A,B,C三个小区的志愿者人数分别为60,40,20,现采用分层抽样的方法从这120名志愿者中随机抽取6人去支援夕阳红敬老院.若再从这6人中随机抽取2名作为负责人,则这2名志愿者来自不同小区的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com