
【题目】已知函数![]() ,其中m为常数,且
,其中m为常数,且![]() 是函数
是函数![]() 的极值点.
的极值点.
(Ⅰ)求m的值;
(Ⅰ)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)先对![]() 求导,再利用
求导,再利用![]() ,列式求解
,列式求解![]() ,最后再进行检验即可;
,最后再进行检验即可;
(Ⅱ)令![]() ,则题意可转化为
,则题意可转化为![]() 在
在![]() 上恒成立,对
上恒成立,对![]() 求导,然后分
求导,然后分![]() ,
,![]() 和
和![]() 三种情况,研究
三种情况,研究![]() 的单调性,判断其最小值是否大于0,从而得出结论.
的单调性,判断其最小值是否大于0,从而得出结论.
(Ⅰ)![]() ,则
,则![]() ,
,
![]() 是函数
是函数![]() 的极值点,
的极值点,
![]() ,
,![]() ,
,
又![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,![]() 上单调递减,
上单调递减,
∴![]() 是函数
是函数![]() 的极大值点,
的极大值点,
∴![]() 符合题意;
符合题意;
(Ⅱ)令![]() ,则
,则![]() ,
,
由题得![]() 在
在![]() 上恒成立,
上恒成立,
![]() ,
,
令![]() ,
,
则![]() ,
,
①当![]() 时,
时,![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,∴
上单调递增,∴![]() ,成立;
,成立;
②当![]() 时,令
时,令![]() ,
,
则![]() ,
,
在![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
则在![]() 上存在唯一
上存在唯一![]() 使得
使得![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,不符合题意;
,不符合题意;
③当![]() 时,在
时,在![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,此时
上单调递减,此时![]() ,不符合题意;
,不符合题意;
综上所述,实数k的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的上下顶点分别为
的上下顶点分别为![]() ,
,![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,与
两点,与![]() 相交于点
相交于点![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若![]() ,求
,求![]() 面积的最大值;
面积的最大值;
(Ⅲ)设直线![]() ,
,![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某精密仪器生产厂准备购买![]() ,
,![]() ,
,![]() 三种型号数控车床各一台,已知这三台车床均使用同一种易损件.在购进机器时,可以额外购买这种易损件作为备件,每个0.1万元.在机器使用期间,如果备件不足再购买,则每个0.2万元.现需要决策在购买机器时应同时购买几个易损件,为此搜集并整理了三种型号各120台车床在一年使用期内更换的易损零件数,得到如下统计表:
三种型号数控车床各一台,已知这三台车床均使用同一种易损件.在购进机器时,可以额外购买这种易损件作为备件,每个0.1万元.在机器使用期间,如果备件不足再购买,则每个0.2万元.现需要决策在购买机器时应同时购买几个易损件,为此搜集并整理了三种型号各120台车床在一年使用期内更换的易损零件数,得到如下统计表:
每台车床在一年中更换易损件的件数 | 5 | 6 | 7 | |
频数 |
| 60 | 60 | 0 |
| 30 | 60 | 30 | |
| 0 | 80 | 40 | |
将调查的每种型号车床在一年中更换的易损件的频率视为概率,每台车床在易损件的更换上相互独立.
(Ⅰ)求一年中![]() ,
,![]() ,
,![]() 三种型号车床更换易损件的总数超过18件的概率;
三种型号车床更换易损件的总数超过18件的概率;
(Ⅱ)以一年购买易损件所需总费用的数学期望为决策依据,问精密仪器生产厂在购买车床的同时应购买18件还是19件易损件?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图统计了截止到2019年年底中国电动汽车充电桩细分产品占比及保有量情况,关于这5次统计,下列说法正确的是( )
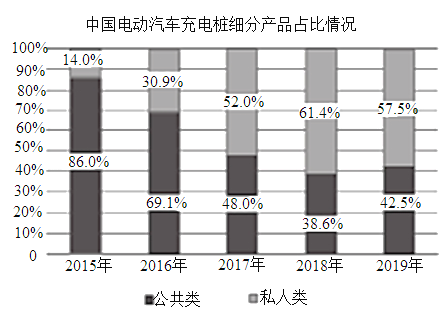
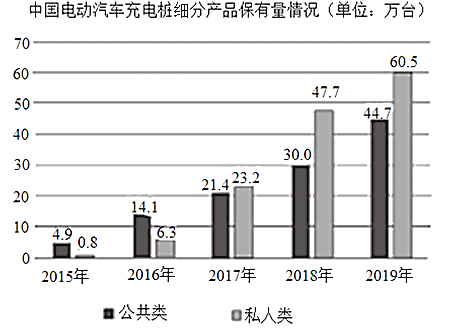
A.私人类电动汽车充电桩保有量增长率最高的年份是2018年
B.公共类电动汽车充电桩保有量的中位数是25.7万台
C.公共类电动汽车充电桩保有量的平均数为23.12万台
D.从2017年开始,我国私人类电动汽车充电桩占比均超过50%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() (
(![]() )的离心率
)的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过
,过![]() ,
,![]() 分别作两条相互垂直的直线
分别作两条相互垂直的直线![]() ,
,![]() ,分别交椭圆
,分别交椭圆![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 的交点为
的交点为![]() ,三角形
,三角形![]() 面积的最大值为1.
面积的最大值为1.
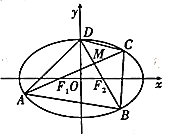
(1)求椭圆![]() 的方程;
的方程;
(2)当四边形![]() 的面积
的面积![]() 最小时,求点
最小时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】精准扶贫点用2400元的资金为贫困户购买良种羊羔,共有肉用山羊、毛用绵羊、产奶山羊三种羊羔,价格均为每只300元,若要求每种羊羔至少买1只,则所有可能的购买方案总数为( )
A.12B.14C.21D.18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2012年12月18日,作为全国首批开展空气质量新标准监测的74个城市之一,郑州市正式发布![]() 数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(
数据.资料表明,近几年来,郑州市雾霾治理取得了很大成效,空气质量与前几年相比得到了很大改善.郑州市设有9个监测站点监测空气质量指数(![]() ),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的
),其中在轻度污染区、中度污染区、重度污染区分别设有2,5,2个监测站点,以9个站点测得的![]() 的平均值为依据,播报我市的空气质量.
的平均值为依据,播报我市的空气质量.
(1)若某日播报的![]() 为118,已知轻度污染区
为118,已知轻度污染区![]() 的平均值为74,中度污染区
的平均值为74,中度污染区![]() 的平均值为114,求重度污染区
的平均值为114,求重度污染区![]() 的平均值;
的平均值;
(2)如图是2018年11月的30天中![]() 的分布,11月份仅有一天
的分布,11月份仅有一天![]() 在
在![]() 内.
内.
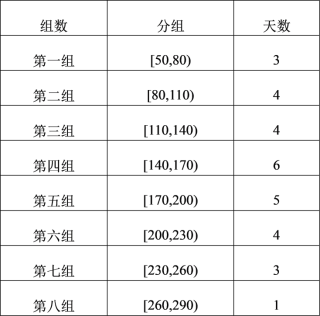
①郑州市某中学利用每周日的时间进行社会实践活动,以公布的![]() 为标准,如果
为标准,如果![]() 小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
小于180,则去进行社会实践活动.以统计数据中的频率为概率,求该校周日进行社会实践活动的概率;
②在“创建文明城市”活动中,验收小组把郑州市的空气质量作为一个评价指标,从当月的空气质量监测数据中抽取3天的数据进行评价,设抽取到![]() 不小于180的天数为
不小于180的天数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com