
分析 (1)根据条件得到B⊆A,从而可讨论B是否为空集,从而得出关于m的不等式或不等式组,得出m的范围求并集即可得出实数m的取值范围;
(2)由x∈Z即可得出集合A={-2,-1,0,1,2,3,4,5},根据组合及二项式定理即可求出A的非空真子集的个数;
(3)根据A∩B=∅即可得到m+1>5,或2m-1<-2,从而便可得出实数m的取值范围.
解答 解:(1)∵A∪B=A;
∴B⊆A;
∴①B=∅时,m+1>2m-1;
∴m<2;
②B≠∅时,$\left\{\begin{array}{l}{m+1≤2m-1}\\{m+1≥-2}\\{2m-1≤5}\end{array}\right.$;
∴2≤m≤3;
∴实数m的取值范围为(-∞,3];
(2)若x∈Z,则A={-2,-1,0,1,2,3,4,5};
∴A的非空子集的个数为${{C}_{8}}^{1}+{{C}_{8}}^{2}+{{C}_{8}}^{3}+{{C}_{8}}^{4}+{{C}_{8}}^{5}+{{C}_{8}}^{6}$$+{{C}_{8}}^{7}={2}^{8}-2=254$;
(3)∵A∩B=∅;
∴m+1>5或2m-1<-2;
∴m>4,或m$<-\frac{1}{2}$;
∴实数m的取值范围为$(-∞,-\frac{1}{2})∪(4,+∞)$.
点评 考查列举法、描述法表示集合的定义及表示形式,并集、交集的概念及子集的概念,元素与集合的关系.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 64π | D. | 128π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
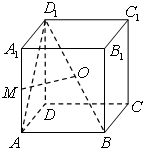 已知正方体ABCD-A1B1C1D1的棱长为1,点O是BD1的中点,M是棱AA1上的一点,请问:
已知正方体ABCD-A1B1C1D1的棱长为1,点O是BD1的中点,M是棱AA1上的一点,请问:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com