
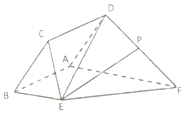
 如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,∠EBA=90°,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$,P为DF的中点.
如图,已知菱形ABCD与直角梯形ABEF所在的平面互相垂直,其中BE∥AF,∠EBA=90°,AB=BE=$\frac{1}{2}$AF=2,∠CBA=$\frac{π}{3}$,P为DF的中点.分析 (1)取AD 的中点M,连接PM,BM,通过证明四边形BMPE是平行四边形得出PE∥BM,故而PE∥平面ABCD;
(2)作出线面角,用λ表示出所作直角三角形的边长,列方程解出λ.
解答 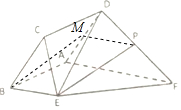 解:(1)取AD 的中点M,连接PM,BM,
解:(1)取AD 的中点M,连接PM,BM,
∵P是DF的中点,M是AD的中点,
∴PM∥AF,PM=$\frac{1}{2}$AF,
又BE∥AF,BE=$\frac{1}{2}$AF,
BE∥PM,BE=PM,
∴四边形BEPM是平行四边形,
∴PE∥BM,又PE?平面ABCD,BM?平面ABCD,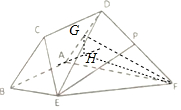
∴PE∥平面ABCD.
(2)过G作GH⊥BA,交BA延长线于H,连接FH,FG,
∵平面ABCD⊥平面ABEF,平面ABCD∩平面ABEF=AB,GH⊥AB,GH?平面ABCD,
∴GH⊥平面ABCD,
∴∠GFH为直线FG与平面ABEF所成角.
∵$\overrightarrow{AG}=λ\overrightarrow{AD}$,∴AG=2λ,∵∠CBA=∠DAH=$\frac{π}{3}$,
∴GH=AG$•sin\frac{π}{3}$=$\sqrt{3}λ$,AH=AG•cos$\frac{π}{3}$=λ,
∴HF=$\sqrt{A{F}^{2}+A{H}^{2}}$=$\sqrt{16+{λ}^{2}}$,FG=$\sqrt{G{H}^{2}+F{H}^{2}}$=2$\sqrt{4+{λ}^{2}}$,
∴sin∠GFH=$\frac{GH}{FG}$=$\frac{\sqrt{3}λ}{2\sqrt{4+{λ}^{2}}}$=$\frac{\sqrt{39}}{26}$.
解得λ=$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面平行的判定,线面角的计算,寻找平行关系,作出线面角的平面角是解题关键,属于中档题.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (4,+∞) | C. | (-1,4) | D. | (-4,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
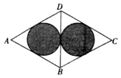 如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )
如图所示,已知菱形ABCD是由等边△ABD与等边△BCD拼接而成,两个小圆与△ABD以及△BCD分别相切,则往菱形ABCD内投掷一个点,该点落在阴影部分内的概率为( )| A. | $\frac{\sqrt{3}}{9π}$ | B. | $\frac{\sqrt{3}}{18π}$ | C. | $\frac{\sqrt{3}π}{18}$ | D. | $\frac{\sqrt{3}π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{e})$ | B. | $(0,\frac{1}{2e})$ | C. | $[\frac{ln3}{3},\frac{1}{e})$ | D. | $[\frac{ln3}{3},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
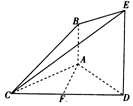 如图,在梯形ADEB中,AB∥DE,AD=DE=2AB,△ACD是正三角形,AB⊥平面ACD,且F是CD的中点.
如图,在梯形ADEB中,AB∥DE,AD=DE=2AB,△ACD是正三角形,AB⊥平面ACD,且F是CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,4) | C. | (0,1)∪(1,+∞) | D. | (0,1)∪(1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com