
 如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
如图,四棱锥P-ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.分析 (1)取AD中点O,由题意可证AD⊥平面POC,可证PC⊥AD;
(2)点D到平面PAM的距离即点D到平面PAC的距离,可证PO为三棱锥P-ACD的体高.设点D到平面PAC的距离为h,由VD-PAC=VP-ACD可得h的方程,解方程可得.
解答  解:(1)取AD中点O,连结OP,OC,AC,依题意可知△PAD,△ACD均为正三角形,
解:(1)取AD中点O,连结OP,OC,AC,依题意可知△PAD,△ACD均为正三角形,
∴OC⊥AD,OP⊥AD,又OC∩OP=O,OC?平面POC,OP?平面POC,
∴AD⊥平面POC,又PC?平面POC,∴PC⊥AD.
(2)点D到平面PAM的距离即点D到平面PAC的距离,
由(1)可知PO⊥AD,又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,PO?平面PAD,
∴PO⊥平面ABCD,即PO为三棱锥P-ACD的体高.
在Rt△POC中,$PO=OC=\sqrt{3}$,$PC=\sqrt{6}$,
在△PAC中,PA=AC=2,$PC=\sqrt{6}$,边PC上的高AM=$\sqrt{P{A^2}-P{M^2}}=\frac{{\sqrt{10}}}{2}$,
∴△PAC的面积${S_{△PAC}}=\frac{1}{2}PC•AM=\frac{1}{2}×\sqrt{6}×\frac{{\sqrt{10}}}{2}=\frac{{\sqrt{15}}}{2}$,
设点D到平面PAC的距离为h,由VD-PAC=VP-ACD得$\frac{1}{3}{S_{△PAC}}•h=\frac{1}{3}{S_{△ACD}}•PO$,
又${S_{△ACD}}=\frac{{\sqrt{3}}}{4}×{2^2}=\sqrt{3}$,∴$\frac{1}{3}×\frac{{\sqrt{15}}}{2}•h=\frac{1}{3}×\sqrt{3}×\sqrt{3}$,
解得$h=\frac{{2\sqrt{15}}}{5}$,∴点D到平面PAM的距离为$\frac{{2\sqrt{15}}}{5}$.
点评 本题考查点线面间的距离计算,涉及棱锥的结构特征以及垂直关系的证明和应用,属中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
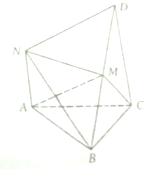 如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)
如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC为直角三角形,∠BAC=90°,PA⊥平面ABC,A为垂足.PC与底面成30°角,且AB=a,AC=2a.
如图,△ABC为直角三角形,∠BAC=90°,PA⊥平面ABC,A为垂足.PC与底面成30°角,且AB=a,AC=2a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且C上任意一点到两个焦点的距离之和都为4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且C上任意一点到两个焦点的距离之和都为4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=$\sqrt{6}$,四边形ABCD是边长为2的菱形,∠ABC=60°,M,N分别为BC和PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
| 温差x (度) | 10 | 11 | 13 | 12 | 9 |
| 发芽数y(颗) | 15 | 16 | 17 | 14 | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com