
【题目】已知常数![]() ,函数
,函数![]() .
.
(1)讨论![]() 在区间
在区间![]() 上的单调性;
上的单调性;
(2)若![]() 存在两个极值点
存在两个极值点![]() ,且
,且![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】试题分析:
(1)结合函数的解析式可得![]() ,分类讨论有:
,分类讨论有:
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,
上单调递减,
在区间![]() 上单调递增;
上单调递增;
(2)首先确定![]() ,结合题意构造函数
,结合题意构造函数![]() ,结合函数
,结合函数![]() 的性质讨论计算可得a的取值范围是
的性质讨论计算可得a的取值范围是![]() .
.
试题解析:
(1)![]()
当![]() 时,此时
时,此时![]() ,
,![]() 在区间
在区间![]() 上单调递增
上单调递增
当![]() 时,
时,![]() ,得
,得![]()
当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;
故![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增
上单调递增
综上所述,当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增
上单调递增
(2)由(1)知,当![]() 时,
时,![]() ,
,
此时![]() 不存在极值点,因而要使得
不存在极值点,因而要使得![]() 有两个极值点,必有
有两个极值点,必有![]()
又![]() 的极值点只可能是
的极值点只可能是![]() ,且由
,且由![]() 的定义域可知
的定义域可知
![]() ,所以
,所以![]()
解得![]() ,此时
,此时![]() 分别是
分别是![]() 的极小值点和极大值点,而
的极小值点和极大值点,而
![]()
![]()
![]()
令![]() 由
由![]() 且
且![]() 知
知![]() 时,当
时,当![]() ,时,
,时,![]()
记![]()
当![]() ,
,![]() ,所以
,所以![]()
因此,![]() 在区间
在区间![]() 上单调递减,从而
上单调递减,从而![]() 故当
故当![]() 时,
时,![]()
当![]() ,
,![]() ,所以
,所以![]()
因此,![]() 在区间
在区间![]() 上单调递减,从而
上单调递减,从而![]()
故当![]() 时,
时,![]()
综上所述,满足条件的a的取值范围为![]()


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在![]() 中,斜边
中,斜边![]() ,将
,将![]() 沿直线
沿直线![]() 旋转得到
旋转得到![]() ,设二面角
,设二面角![]() 的大小为
的大小为![]() .
.
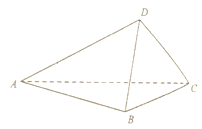
(1)取![]() 的中点
的中点![]() ,过点
,过点![]() 的平面与
的平面与![]() 分别交于点
分别交于点![]() ,当平面
,当平面![]() 平面
平面![]() 时,求
时,求![]() 的长(2)当
的长(2)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司10位员工的月工资(单位:元)为x1 , x2 , …,x10 , 其均值和方差分别为 ![]() 和s2 , 若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
和s2 , 若从下月起每位员工的月工资增加100元,则这10位员工下月工资的均值和方差分别为( )
A.![]() ,s2+1002
,s2+1002
B.![]() +100,s2+1002
+100,s2+1002
C.![]() ,s2
,s2
D.![]() +100,s2
+100,s2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将三项式(x2+x+1)n展开,当n=1,2,3,…时,得到如下所示的展开式,如图所示的广义杨辉三角形: (x2+x+1)0=1
(x2+x+1)1=x2+x+1
(x2+x+1)2=x4+2x3+3x2+2x+1
(x2+x+1)3=x6+3x5+6x4+7x3+6x2+3x+1
观察多项式系数之间的关系,可以仿照杨辉三角形构造如图所示的广义杨辉三角形,其构造方法:第0行为1,以下各行每个数是它头上与左右两肩上3数(不足3数的,缺少的数计为0)之和,第k行共有2k+1个数.若在(a+x)(x2+x+1)4的展开式中,x6项的系数为46,则实数a的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a. 
(1)求证:AB1⊥BC1;
(2)求二面角B﹣AB1﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件。已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com