
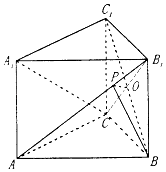
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠ACB=90°.BC=CC1=a,AC=2a. 
(1)求证:AB1⊥BC1;
(2)求二面角B﹣AB1﹣C的正弦值.
【答案】
(1)证明:∵ABC﹣A1B1C1是直三棱柱,
∴CC1⊥平面ABC,则AC⊥CC1.
又∵AC⊥BC,BC∩CC1=C,
∴AC⊥平面B1BCC1,则AC⊥BC1,
∵BC=CC1,∴四边形B1BCC1是正方形,
∴BC1⊥B1C,
又AC∩B1C=C,∴BC1⊥平面AB1C,则AB1⊥BC1
(2)解:设BC1∩B1C=O,作OP⊥AB1于点P,连结BP.
由(1)知BO⊥AB1,而BO∩OP=O,
∴AB1⊥平面BOP,则BP⊥AB1,
∴∠OPB是二面角B﹣AB1﹣C的平面角.
∵△OPB1~△ACB1,∴ ![]() ,
,
∵BC=CC1=a,AC=2a,∴OP= ![]() ,
,
∴ ![]() =
= ![]() .
.
在Rt△POB中,sin∠OPB= 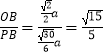 ,
,
∴二面角B﹣AB1﹣C的正弦值为 ![]() .
.
【解析】(1)由已知可得AC⊥平面B1BCC1 , 则AC⊥BC1 , 再由BC=CC1 , 得BC1⊥B1C,由线面垂直的判定可得BC1⊥平面AB1C,从而得到AB1⊥BC1;(2)设BC1∩B1C=O,作OP⊥AB1于点P,连结BP.由(1)知BO⊥AB1 , 进一步得到AB1⊥平面BOP,说明∠OPB是二面角B﹣AB1﹣C的平面角.然后求解直角三角形得答案.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x),满足f(1)=0,且在(0,+∞)上单调递增,则xf(x)>0的解集为( )
A.{x|x<﹣1或x>1}
B.{x|0<x<1或﹣1<x<0}
C.{x|0<x<1或x<﹣1}
D.{x|﹣1<x<0或x>1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题: ①函数y=sin( ![]() ﹣2x)是偶函数;
﹣2x)是偶函数;
②方程x= ![]() 是函数y=sin(2x+
是函数y=sin(2x+ ![]() )的图象的一条对称轴方程;
)的图象的一条对称轴方程;
③若α、β是第一象限角,且α>β,则sinα>sinβ;
④设x1、x2是关于x的方程|logax|=k(a>0,a≠1,k>0)的两根,则x1x2=1;
其中正确命题的序号是 . (填出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax(a>0且a≠1)的图象经过点(2, ![]() ).
).
(1)比较f(2)与f(b2+2)的大小;
(2)求函数g(x)=a ![]() (x≥0)的值域.
(x≥0)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下几个命题中真命题的序号为 .
①在空间中,m、n是两条不重合的直线,α、β是两个不重合的平面,如果α⊥β,α∩β=n,m⊥n,那么m⊥β;
②相关系数r的绝对值越接近于1,两个随机变量的线性相关性越强;
③用秦九昭算法求多项式f(x)=208+9x2+6x4+x6在x=﹣4时,v2的值为22;
④过抛物线y2=4x的焦点作直线与抛物线相交于A、B两点,则使它们的横坐标之和等于4的直线有且只有两条.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于x的不等式 ![]() >1+
>1+ ![]() (其中k∈R,k≠0).
(其中k∈R,k≠0).
(1)若x=3在上述不等式的解集中,试确定k的取值范围;
(2)若k>1时,上述不等式的解集是x∈(3,+∞),求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com