
ΓΨΧβΡΩΓΩΈΣΝΥ―–ΨΩΙψ¥σ –ΟώΕ‘Ι≤œμΒΞ≥ΒΒΡ Ι”Ο«ιΩω,Ρ≥ΙΪΥΨ‘ΎΈ“ –ΥφΜζ≥ι»ΓΝΥ100Οϊ”ΟΜßΫχ––Βς≤ιΘ§ΒΟΒΫ»γœ¬ ΐΨίΘΚ
ΟΩ÷ή Ι”Ο¥Έ ΐ | 1¥Έ | 2¥Έ | 3¥Έ | 4¥Έ | 5¥Έ | 6¥ΈΦΑ“‘…œ |
Ρ– | 4 | 3 | 3 | 7 | 8 | 30 |
š | 6 | 5 | 4 | 4 | 6 | 20 |
ΚœΦΤ | 10 | 8 | 7 | 11 | 14 | 50 |
»œΈΣΟΩ÷ή Ι”Ο≥§Ιΐ3¥ΈΒΡ”ΟΜßΈΣΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±.
(1)Ζ÷±πΙάΥψΡ–ΓΔ≈°ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡΗ≈¬ ΘΜ
(2)«κΆξ≥…œ¬ΟφΒΡ2ΓΝ2Ν–ΝΣ±μ,≤Δ≈–ΕœΡήΖώ”–95%Α―Έ’,»œΈΣ «ΖώΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±”κ–‘±π”–ΙΊ.
≤Μœ≤ΜΕΤοΙ≤œμΒΞ≥Β | œ≤ΜΕΤοΙ≤œμΒΞ≥Β | ΚœΦΤ | |
Ρ– | |||
š | |||
ΚœΦΤ |
ΗΫ±μΦΑΙΪ ΫΘΚ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() .
.
| 0.15 | 0Θ°10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ΓΨ¥πΑΗΓΩΘ®1Θ©Ρ–”ΟΜß÷–ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡΗ≈¬ ΒΡΙάΦΤ÷ΒΈΣ![]() Θ§≈°”ΟΜß÷–ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡΗ≈¬ ΒΡΙάΦΤ÷ΒΈΣ
Θ§≈°”ΟΜß÷–ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡΗ≈¬ ΒΡΙάΦΤ÷ΒΈΣ![]() Θ®2Θ©Χν±μΦϊΫβΈωΘ§ΟΜ”–95%ΒΡΑ―Έ’»œΈΣ «ΖώΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±”κ–‘±π”–ΙΊ
Θ®2Θ©Χν±μΦϊΫβΈωΘ§ΟΜ”–95%ΒΡΑ―Έ’»œΈΣ «ΖώΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±”κ–‘±π”–ΙΊ
ΓΨΫβΈωΓΩ
(1)άϊ”ΟΙ≈ΒδΗ≈–ΆΒΡΗ≈¬ ΙάΥψΡ–ΓΔ≈°ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡΗ≈¬ ΘΜΘ®2Θ©œ»Άξ≥…![]() Ν–ΝΣ±μΘ§‘Όάϊ”ΟΕάΝΔ–‘Φλ―ι≈–ΕœΡήΖώ”–95%Α―Έ’,»œΈΣ «ΖώΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±”κ–‘±π”–ΙΊ.
Ν–ΝΣ±μΘ§‘Όάϊ”ΟΕάΝΔ–‘Φλ―ι≈–ΕœΡήΖώ”–95%Α―Έ’,»œΈΣ «ΖώΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±”κ–‘±π”–ΙΊ.
Ϋβ:(1)”…Βς≤ι ΐΨίΩ…÷Σ,Ρ–”ΟΜß÷–ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡ±»¬ ΈΣ![]() Θ§
Θ§
“ρ¥ΥΡ–”ΟΜß÷–ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡΗ≈¬ ΒΡΙάΦΤ÷ΒΈΣ![]() .
.
≈°”ΟΜß÷–ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡ±»¬ ΈΣ![]() Θ§
Θ§
“ρ¥Υ≈°”ΟΜß÷–ΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±ΒΡΗ≈¬ ΒΡΙάΦΤ÷ΒΈΣ![]() .
.
Θ®2Θ©”…ΆΦ÷–±μΗώΩ…ΒΟ![]() Ν–ΝΣ±μ»γœ¬ΘΚ
Ν–ΝΣ±μ»γœ¬ΘΚ
≤Μœ≤ΜΕΤοΙ≤œμΒΞ≥Β | œ≤ΜΕΤοΙ≤œμΒΞ≥Β | ΚœΦΤ | |
Ρ– | 10 | 45 | 55 |
š | 15 | 30 | 45 |
ΚœΦΤ | 25 | 75 | 100 |
ΫΪ![]() Ν–ΝΣ±μ¥ζ»κΙΪ ΫΦΤΥψΒΟΘΚ
Ν–ΝΣ±μ¥ζ»κΙΪ ΫΦΤΥψΒΟΘΚ
![]()
Υυ“‘ΟΜ”–95%ΒΡΑ―Έ’»œΈΣ «ΖώΓΑœ≤ΜΕΤοΙ≤œμΒΞ≥ΒΓ±”κ–‘±π”–ΙΊ.


 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚ· ΐ![]() Θ®Τδ÷–
Θ®Τδ÷–![]() Θ§
Θ§![]() ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©Θ°
ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐΘ©Θ°
ΔΌ![]() Θ§ ΙΒΟ÷±œΏ
Θ§ ΙΒΟ÷±œΏ![]() ΈΣΚ· ΐ
ΈΣΚ· ΐ![]() ΒΡ“ΜΧθ«–œΏΘΜ
ΒΡ“ΜΧθ«–œΏΘΜ
ΔΎΕ‘![]() Θ§Κ· ΐ
Θ§Κ· ΐ![]() ΒΡΒΦΚ· ΐ
ΒΡΒΦΚ· ΐ![]() ΈόΝψΒψΘΜ
ΈόΝψΒψΘΜ
ΔέΕ‘![]() Θ§Κ· ΐ
Θ§Κ· ΐ![]() Ήή¥φ‘ΎΝψΒψΘΜ
Ήή¥φ‘ΎΝψΒψΘΜ
‘ρ…œ ωΫα¬έ’ΐ»ΖΒΡ «______Θ°Θ®–¥≥ωΥυ”–’ΐ»ΖΒΡΫα¬έΒΡ–ρΚ≈Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ¥σΤχΈέ»Ψ «Έ“ΙζΡΩ«ΑΉνΆΜ≥ωΒΡΜΖΨ≥Έ Χβ÷°“ΜΘ§Τδ÷–ΙΛ≥ßΖœΤχ «¥σΤχΈέ»ΨΒΡ÷Ί¥σΈέ»Ψ‘¥÷°“ΜΓΘΙΛ≥ßΖœΤχΈ¥Ψ≠ΨΜΜ·¥Πάμ≈≈Ζ≈÷ΝΩ’Τχ÷–Θ§≥ΐΝΥΕ‘Ω’Τχ÷ ΝΩ‘λ≥…―œ÷ΊΤΤΜΒΘ§ΜΙΜαΕ‘»ΥΧεΒΡΫΓΩΒ‘λ≥…÷Ί¥σΆΰ–≤ΓΘ≥ΛΤΎ…ζΜν‘ΎΈέ»ΨΒΡΩ’Τχ÷–Θ§…ζΜν÷ ΝΩΦΑ…μΧεΫΓΩΒΫΪΦ±Ψγœ¬ΫΒΓΘΡ≥ΙΛ≥ß“ρΈΣΈέ»ΨΈ Χβ–ηΗΡΫχΦΦ θΘ§2019Ρξ≥θΙΚΫχ“ΜΧ®ΜΖ±Θ–¬ΜζΤςΆΕ»κ…ζ≤ζΘ§ΜζΤςΒΡ≥…±ΨΦέΈΣ36Άρ‘ΣΘ§ΒΎ![]() ΡξΗΟΜζΤςΑϋά®Έ§–όΖ―ΚΆΜζΤςΜΛάμΖ―”Ο‘ΎΡΎΘ§ΟΩΡξΝμ–ηΆΕ»ΥΖ―”Ο
ΡξΗΟΜζΤςΑϋά®Έ§–όΖ―ΚΆΜζΤςΜΛάμΖ―”Ο‘ΎΡΎΘ§ΟΩΡξΝμ–ηΆΕ»ΥΖ―”Ο![]() Άρ‘ΣΘ§ΙΚΫχΗΟΜζΤςΚσΟΩΡξ”·άϊ20Άρ‘ΣΘ°
Άρ‘ΣΘ§ΙΚΫχΗΟΜζΤςΚσΟΩΡξ”·άϊ20Άρ‘ΣΘ°
Θ®1Θ©Έ ΗΟΜζΤςΆΕ»κ…ζ≤ζΒΎΦΗΡξΘ§ΙΛ≥ßΩΣ Φ”·άϊΘ®Φ¥Ήή ’»κ¥σ”ΎΥυ”–ΆΕ»ΥΒΡΖ―”ΟΘ©?
Θ®2Θ©”…”ΎΜζΤς Ι”ΟΡξœό‘Ϋ¥σΈ§–όΒ»Ζ―”Ο‘ΫΗΏΘ§Υυ“‘ΙΛ≥ßΨωΕ®Β±ΡξΤΫΨυάϊ»σΉν¥σ ±ΫΪΗΟΜζΤς“‘5Άρ‘ΣΒΆΦέ¥ΠάμΘ§Έ Ι”ΟΗΟΜζΤςΦΗΡξΚσΙΛ≥ßΡξΤΫΨυάϊ»σΉν¥σ?¥Υ ±ΙΛ≥ßΜώΒΟΒΡΉήάϊ»σΈΣΕύ…Ό?
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() «Ε®“ε‘Ύ
«Ε®“ε‘Ύ![]() …œΒΡΤφΚ· ΐΘ§Β±
…œΒΡΤφΚ· ΐΘ§Β±![]() ±Θ§
±Θ§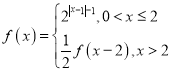 Θ§‘ρΚ· ΐ
Θ§‘ρΚ· ΐ![]() ‘Ύ
‘Ύ![]() …œΒΡΥυ”–ΝψΒψ÷°ΚΆΈΣΘ® Θ©
…œΒΡΥυ”–ΝψΒψ÷°ΚΆΈΣΘ® Θ©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψ![]() «‘≤
«‘≤![]() ΘΚ
ΘΚ![]() …œΒΡ“ΜΕ·ΒψΘ§Βψ
…œΒΡ“ΜΕ·ΒψΘ§Βψ![]() Θ§Βψ
Θ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œΘ§«“¬ζΉψ
…œΘ§«“¬ζΉψ![]() .
.
Θ®1Θ©«σΒψ![]() ΒΡΙλΦΘ
ΒΡΙλΦΘ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η«ζœΏ![]() ”κ
”κ![]() ÷αΒΡ’ΐΑκ÷αΘ§
÷αΒΡ’ΐΑκ÷αΘ§![]() ÷αΒΡ’ΐΑκ÷αΒΡΫΜΒψΖ÷±πΈΣΒψ
÷αΒΡ’ΐΑκ÷αΒΡΫΜΒψΖ÷±πΈΣΒψ![]() Θ§
Θ§![]() Θ§–±¬ ΈΣ
Θ§–±¬ ΈΣ![]() ΒΡΕ·÷±œΏ
ΒΡΕ·÷±œΏ![]() ΫΜ«ζœΏ
ΫΜ«ζœΏ![]() ”Ύ
”Ύ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§Τδ÷–Βψ
ΝΫΒψΘ§Τδ÷–Βψ![]() ‘ΎΒΎ“ΜœσœόΘ§«σΥΡ±Ώ–Έ
‘ΎΒΎ“ΜœσœόΘ§«σΥΡ±Ώ–Έ![]() ΟφΜΐΒΡΉν¥σ÷Β.
ΟφΜΐΒΡΉν¥σ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΥΡ±Ώ–Έ![]() «±Ώ≥ΛΈΣ2ΒΡΝβ–ΈΘ§
«±Ώ≥ΛΈΣ2ΒΡΝβ–ΈΘ§![]() Θ§
Θ§![]() ΈΣ
ΈΣ![]() ΒΡ÷–ΒψΘ§“‘
ΒΡ÷–ΒψΘ§“‘![]() ΈΣ’έΚέΫΪ
ΈΣ’έΚέΫΪ![]() ’έΤπΒΫ
’έΤπΒΫ![]() ΒΡΈΜ÷ΟΘ§ ΙΒΟΤΫΟφ
ΒΡΈΜ÷ΟΘ§ ΙΒΟΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ§»γΆΦ2.
Θ§»γΆΦ2.

Θ®1Θ©÷ΛΟςΘΚΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©«σΕΰΟφΫ«![]() ΒΡ”ύœ“÷Β.
ΒΡ”ύœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() œύ«–”ΎΒΎ“ΜœσœόΒΡΒψ
œύ«–”ΎΒΎ“ΜœσœόΒΡΒψ![]() Θ§«“÷±œΏ
Θ§«“÷±œΏ![]() ”κ
”κ![]() ÷αΘ§
÷αΘ§![]() ÷αΖ÷±πΫΜ”ΎΒψ
÷αΖ÷±πΫΜ”ΎΒψ![]() Θ§
Θ§![]() Θ§Β±
Θ§Β±![]() Θ®
Θ®![]() ΈΣΉχ±ξ‘≠ΒψΘ©ΒΡΟφΜΐΉν–Γ ±Θ§
ΈΣΉχ±ξ‘≠ΒψΘ©ΒΡΟφΜΐΉν–Γ ±Θ§![]() Θ®
Θ®![]() Θ§
Θ§![]() ΈΣΆ÷‘≤ΒΡΝΫΗωΫΙΒψΘ©Θ§‘ρ¥Υ ±
ΈΣΆ÷‘≤ΒΡΝΫΗωΫΙΒψΘ©Θ§‘ρ¥Υ ±![]() ÷–
÷–![]() ΒΡΤΫΖ÷œΏΒΡ≥ΛΕ»ΈΣΘ® Θ©
ΒΡΤΫΖ÷œΏΒΡ≥ΛΕ»ΈΣΘ® Θ©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΈΣ
ΒΡάκ–Ρ¬ ΈΣ![]() Θ§Ά÷‘≤
Θ§Ά÷‘≤![]() ΒΡ≥Λ÷α≥ΛΈΣ4.
ΒΡ≥Λ÷α≥ΛΈΣ4.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©“―÷Σ÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΘ§ «Ζώ¥φ‘Ύ Β ΐ
ΝΫΒψΘ§ «Ζώ¥φ‘Ύ Β ΐ![]() ΙΒΟ“‘œΏΕΈ
ΙΒΟ“‘œΏΕΈ![]() ΈΣ÷±ΨΕΒΡ‘≤«ΓΚΟΨ≠ΙΐΉχ±ξ‘≠Βψ
ΈΣ÷±ΨΕΒΡ‘≤«ΓΚΟΨ≠ΙΐΉχ±ξ‘≠Βψ![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ω
ΘΩ»τ¥φ‘ΎΘ§«σ≥ω![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏCΘΚy2ΘΫ2pxΘ®pΘΨ0Θ©ΒΡΉΦœΏΖΫ≥ΧΈΣxΘΫ©¹1Θ°
Θ®1Θ©«σ≈ΉΈοœΏCΒΡΖΫ≥ΧΘΜ
Θ®2Θ©Ιΐ≈ΉΈοœΏCΒΡΫΙΒψΉς÷±œΏlΘ§ΫΜ≈ΉΈοœΏC”ΎAΘ§BΝΫΒψΘ§»τœΏΕΈAB÷–ΒψΒΡΚαΉχ±ξΈΣ6Θ§«σ|AB|Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com