
已知函数 ,
, .
.
(Ⅰ)设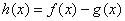 ,求
,求 的单调区间;
的单调区间;
(Ⅱ)若对 ,总有
,总有 成立.
成立.
(1)求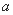 的取值范围;
的取值范围;
(2)证明:对于任意的正整数 ,不等式
,不等式
 恒成立.
恒成立.
解:(Ⅰ)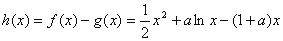 ,定义域为
,定义域为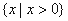 ,
,
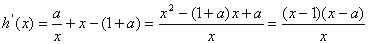 , …… 1分
, …… 1分
(1)当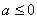 时,令
时,令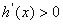 ,
,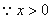 ,
,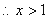 ,
,
令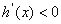 ,
, 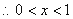 ;
;
(2)当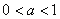 时,令
时,令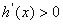 ,则
,则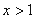 或
或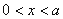 ,
,
令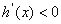 ,
, 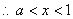 ; …… 3分
; …… 3分
(3)当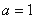 时,
时,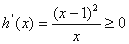 恒成立;
恒成立;
(4)当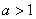 时,令
时,令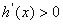 ,则
,则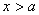 或
或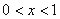 ,
,
令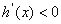 ,
, 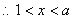 ; …… 4分
; …… 4分
综上:当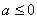 时,
时, 的增区间为
的增区间为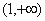 ,
, 的减区间为
的减区间为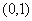 ;
;
当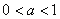 时,
时, 的增区间为
的增区间为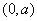 和
和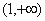 ,
, 的减区间为
的减区间为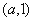 ;
;
当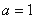 时,
时, 的增区间为
的增区间为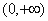 ;
;
当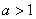 时,
时, 的增区间为
的增区间为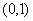 和
和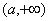 ,
, 的减区间为
的减区间为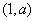 . ……5分
. ……5分
(Ⅱ)(1)由题意,对任意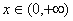 ,
,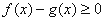 恒成立,即
恒成立,即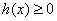 恒成立,
恒成立,
只需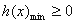 . ……6分
. ……6分
由第(Ⅰ)知:
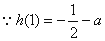 ,显然当
,显然当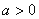 时,
时, 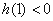 ,此时对任意
,此时对任意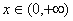 ,
,
不能恒成立; (或者分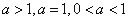 逐个讨论) …… 8分
逐个讨论) …… 8分
当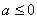 时,
时,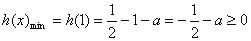 ,
,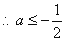 ;
;
综上: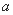 的取值范围为
的取值范围为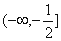 . …… 9分
. …… 9分
(2)证明:由(1)知:当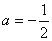 时,
时,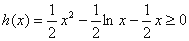 ,……10分
,……10分
即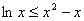 ,当且仅当
,当且仅当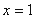 时等号成立.
时等号成立.
当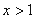 时,可以变换为
时,可以变换为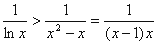 , …… 12分
, …… 12分
在上面的不等式中,令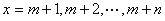 ,则有
,则有

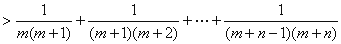
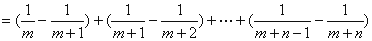
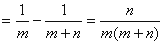
 不等式
不等式
 恒成立.
恒成立.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com