
科目:高中数学 来源: 题型:选择题
| A. | 相切 | B. | 相离 | C. | 相交 | D. | 相切或相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
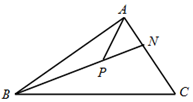 如图,在锐角△ABC中,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,P是线段BN(不含端点)上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,则$\frac{1}{m}$+$\frac{3}{n}$的最小值为16.
如图,在锐角△ABC中,$\overrightarrow{AN}$=$\frac{1}{2}$$\overrightarrow{NC}$,P是线段BN(不含端点)上的一点,若$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$,则$\frac{1}{m}$+$\frac{3}{n}$的最小值为16.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为2,动点P从ABCD顶点A开始,顺次经B,C,D绕边界一周,当x表示点P的行程,f(x)表示线段PA之长时,求f(x)的解析式,并求f(3)的值.
如图,正方形ABCD的边长为2,动点P从ABCD顶点A开始,顺次经B,C,D绕边界一周,当x表示点P的行程,f(x)表示线段PA之长时,求f(x)的解析式,并求f(3)的值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -4 | C. | -2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单位向量都相等 | |
| B. | 长度相等且方向相反的两个向量不一定是共线向量 | |
| C. | 若$\overrightarrow a$,$\overrightarrow b$满足$|{\overrightarrow a}|$>$|{\overrightarrow b}|$且$\overrightarrow a$与$\overrightarrow b$同向,则$\overrightarrow a$>$\overrightarrow b$ | |
| D. | 对于任意向量$\overrightarrow a$,$\overrightarrow b$,必有$|{\overrightarrow a+\overrightarrow b}|$≤$|{\overrightarrow a}|$+$|{\overrightarrow b}|$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com