
 如图,正方形ABCD的边长为2,动点P从ABCD顶点A开始,顺次经B,C,D绕边界一周,当x表示点P的行程,f(x)表示线段PA之长时,求f(x)的解析式,并求f(3)的值.
如图,正方形ABCD的边长为2,动点P从ABCD顶点A开始,顺次经B,C,D绕边界一周,当x表示点P的行程,f(x)表示线段PA之长时,求f(x)的解析式,并求f(3)的值. 分析 分点P在AB上运动、点P在BC上运动、点P在CD上运动以及点P在DA上运动时,求出PA的表达式,用分段函数表示出来即可;把x=3代入对应的函数f(x)的解析式,求值即可.
解答 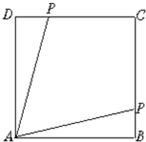 解:如图,当点P在AB上运动时,PA=x,
解:如图,当点P在AB上运动时,PA=x,
即y=x,0≤x≤2;
当点P在BC上运动时,y=$\sqrt{4+(x-2)^{2}}$,2<x≤4;
当点P在CD上运动时,y=$\sqrt{4+(6-x)^{2}}$,4<x≤6;
当点P在DA上运动时,y=6-x,6<x≤8
∴函数f(x)=$\left\{\begin{array}{l}{x,0≤x≤2}\\{\sqrt{4+(x-2)^{2}},2<x≤4}\\{\sqrt{4+(6-x)^{2}},4<x≤6}\\{6-x,6<x≤8}\end{array}\right.$;
f(3)=$\sqrt{4+1}$=$\sqrt{5}$.
点评 本题考查了分段函数模型的应用问题,分段函数是把定义域分成几个适当的区间,在各个区间上对应着不同的解析式.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数f(x)=$\left\{\begin{array}{l}\frac{2}{x},x<-1\\-2,-1≤x<0\\ 3x-2,x≥0\end{array}$,
设函数f(x)=$\left\{\begin{array}{l}\frac{2}{x},x<-1\\-2,-1≤x<0\\ 3x-2,x≥0\end{array}$,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com