练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．已知复数z1=3+i，z2=4+3i
    （1）写出Z1的共轭复数，并求它的模
    （2）求Z1•Z2的值．

    分析 （1）Z1的共轭复数$\overline{{Z}_{1}}$=3-i，利用复数的模的计算公式可得$|\overline{{z}_{1}}|$．
    （2）利用复数的运算法则即可得出．

    解答 解：（1）Z1的共轭复数$\overline{{Z}_{1}}$=3-i，$|\overline{{z}_{1}}|$=$\sqrt{{3}^{2}+（-1）^{2}}$=$\sqrt{10}$．
    （2）Z1•Z2=（3+i）（4+3i）=12-3+13i=9+13i．

    点评 本题考查了复数的运算法则、模的计算公式、共轭复数的定义，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．如图，正方形ABCD的边长为2，动点P从ABCD顶点A开始，顺次经B，C，D绕边界一周，当x表示点P的行程，f（x）表示线段PA之长时，求f（x）的解析式，并求f（3）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知（3+x）10=a0+a1（1+x）+a2（1+x）2+…+a10（1+x）10，则a9=（　　）
    A．20B．21C．31D．32

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知sinx-3cosx=$\sqrt{5}$，则tanx=（　　）
    A．-2或$\frac{1}{2}$B．2或-$\frac{1}{2}$C．2或$\frac{1}{2}$D．-2或-$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．下列命题正确的是（　　）
    A．单位向量都相等
    B．长度相等且方向相反的两个向量不一定是共线向量
    C．若$\overrightarrow a$，$\overrightarrow b$满足$|{\overrightarrow a}|$＞$|{\overrightarrow b}|$且$\overrightarrow a$与$\overrightarrow b$同向，则$\overrightarrow a$＞$\overrightarrow b$
    D．对于任意向量$\overrightarrow a$，$\overrightarrow b$，必有$|{\overrightarrow a+\overrightarrow b}|$≤$|{\overrightarrow a}|$+$|{\overrightarrow b}|$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．证明函数f（x）=3x+2在R上是增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

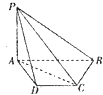    12．如图所示，四棱锥P-ABCD的底面为等腰梯形，AB∥DC，AB=2AD，若PA⊥平面ABCD，∠ABC=60°
    （1）求证：平面PAC⊥平面PBC；
    （2）若PA=AB，求平面PBC与平面PAD所成的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知变量x，y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≤1}\\{x≤y}\end{array}\right.$，则z=2x+y的最大值（　　）
    A．1B．3C．4D．8

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

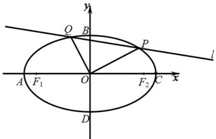    10．如图，在直角坐标系xOy中，椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左右焦点分别为F1，F2，左、右、上、下四个顶点分别为A，C，B，D，四边形F1BF2D的面积与四边形ABCD的面积的比值为$\frac{{\sqrt{6}}}{3}$．
    （1）求椭圆E的离心率；
    （2）设椭圆E的焦距为$2\sqrt{2}$，直线l与椭圆E交于P，Q两点，且OP⊥OQ，求证：直线l恒与一定圆相切，并求出该圆的方程．

    查看答案和解析>>

    同步练习册答案