
分析 (1)由f(x)=$\frac{1}{1-x-{x}^{2}}$,得(1-x-x2)$({a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}+…+{a}_{n}{x}^{n}+…)=1$,然后利用展开式中x,x2的系数为0,常数项为1求得数列{an}的前三项a0、a1、a2的值,再由xn(n≥2)的系数为0得到数列递推式,说明数列为递增数列,从而证得an≥n;
(2)由bn=$\frac{{a}_{n}}{{a}_{n-1}{a}_{n+1}}$,利用裂项相消法求数列{bn}的前n项和为Sn,放大后证得Sn<2,把Sn≤rf(x)恒成立转化为2x2+2x+r-2≥0在x∈D=($\frac{-1-\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$)上恒成立,结合判别式可得满足条件的正常数r存在.
解答 解:(1)由f(x)=$\frac{1}{1-x-{x}^{2}}$=a0+a1x+a2x2+…+anxn+…
得(1-x-x2)$({a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}+…+{a}_{n}{x}^{n}+…)=1$,
显然x,x2的系数为0,常数项为1,
∴a0=1,a1-a0=0,a2-a1-a0=0,
则a0=1,a1=1,a2=2,
考虑xn(n≥2)的系数,则有an-an-1-an-2=0(n≥2),
即an+2=an+1+an,
∴数列{an}单调递增,
又∵a1=1,a2=2,
∴对任意的n∈N*都有an≥n;
(2)bn=$\frac{{a}_{n}}{{a}_{n-1}{a}_{n+1}}$=$\frac{{a}_{n+1}-{a}_{n-1}}{{a}_{n-1}{a}_{n+1}}$=$\frac{1}{{a}_{n-1}}-\frac{1}{{a}_{n+1}}$,
∴Sn=($\frac{1}{{a}_{0}}-\frac{1}{{a}_{2}}$)+($\frac{1}{{a}_{1}}-\frac{1}{{a}_{3}}$)+($\frac{1}{{a}_{2}}-\frac{1}{{a}_{4}}$)+…+($\frac{1}{{a}_{n-1}}-\frac{1}{{a}_{n+1}}$)
=$\frac{1}{{a}_{0}}+\frac{1}{{a}_{1}}-\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$=2-$\frac{1}{{a}_{n}}-\frac{1}{{a}_{n+1}}$<2.
若存在正常数r,使{bn}的前n项和Sn≤rf(x)对任意的x∈D恒成立,
即rf(x)=$\frac{r}{1-x-{x}^{2}}≥2$对任意的x∈D恒成立,
∵1-x-x2>0在x∈D上成立,
也就是r≥2-2x-2x2,即2x2+2x+r-2≥0在x∈D=($\frac{-1-\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$)上恒成立.
∵二次函数y=2x2+2x+r-2的对称轴方程为x=-$\frac{1}{2}$∈($\frac{-1-\sqrt{5}}{2}$,$\frac{-1+\sqrt{5}}{2}$),
则需△=22-8(r-2)=20-8r≤0,
即r$≥\frac{5}{2}$.
故存在正常数r,使{bn}的前n项和Sn≤rf(x)对任意的x∈D恒成立.
点评 本题考查了数列的函数特性,考查了数列递推式,训练了裂项相消法求数列的和,考查了等差数列通项公式的求法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,$\sqrt{2}$+1) | B. | (1,$\sqrt{2}$+1) | C. | (1,$\sqrt{3}$) | D. | $({\sqrt{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
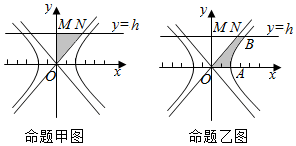
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com