
分析 (Ⅰ)利用正弦定理把题设等式中的角的正弦转化成边,解方程组求得a和c的值.
(Ⅱ)先利用余弦定理求得a,b和c的关系,把题设等式代入表示出p2,进而利用cosB的范围确定p2的范围,进而确定pd 范围.
解答 解:(I)由题设并利用正弦定理,得$\left\{\begin{array}{l}{a+c=\frac{5}{4}}\\{ac=\frac{1}{4}}\end{array}\right.$,
故可知a,c为方程x2-$\frac{5}{4}$x+$\frac{1}{4}$=0的两根,
解得$\left\{\begin{array}{l}{a=1}\\{c=\frac{1}{4}}\end{array}\right.$或$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{c=1}\end{array}\right.$,
(II)由余弦定理,b2=a2+c2-2accosB=(a+c)2-2ac-2accosB=p2b2-$\frac{1}{2}{b}^{2}$-$\frac{1}{2}{b}^{2}$cosB,
即p2=$\frac{3}{2}$$+\frac{1}{2}$cosB,
因为0<cosB<1,可得:p2∈($\frac{3}{2}$,2),p>0,
所以:$\frac{\sqrt{6}}{2}<p<\sqrt{2}$.
点评 本题主要考查了解三角形问题,考查了对正弦定理和余弦定理的公式及变形公式熟练应用,属于中档题.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
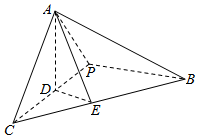 三棱锥A-PBC中,D是线段PC上一点,且AD⊥面BPC,AC=2,BC=3,AB=$\sqrt{7}$,E是BC上一点,且CE=1.
三棱锥A-PBC中,D是线段PC上一点,且AD⊥面BPC,AC=2,BC=3,AB=$\sqrt{7}$,E是BC上一点,且CE=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数非偶函数 | B. | 偶函数非奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既非偶函数又非奇函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{8}$ | B. | $\frac{15}{32}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 3 | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com