
分析 (Ⅰ)a=-1时,求出导函数$f'(x)=ln(x-1)+\frac{x}{x-1}+2x+b$,记g(x)=f'(x)-b,再求解导函数求出极值点,利用函数的单调性,求出最小值,转化为f'(x)=0?g(x)=-b,通过(ⅰ)当b≥ln2-6时,(ⅱ)当$-e-\frac{2}{e}-2<b<ln2-6$时,(ⅲ)当$-2e-\frac{1}{e}-4<b≤-e-\frac{2}{e}-2$时,(ⅳ)当$b≤-2e-\frac{1}{e}-4$时,分别求解函数的极值即可.
(Ⅱ)当a=1,b=e+2时,对任意的x∈(1,+∞)都有$f(x)<k•{e^{\frac{1}{2}x}}$,即$ln(x-1)-x+e+2<k•\frac{{{e^{\frac{x}{2}}}}}{x}$,记h(x)=ln(x-1)-x+e+2,$ϕ(x)=k•\frac{{{e^{\frac{x}{2}}}}}{x}$,通过导函数判断函数的最值,推出结果即可.
解答 解:(Ⅰ)a=-1时,$f'(x)=ln(x-1)+\frac{x}{x-1}+2x+b$,记g(x)=f'(x)-b,
则$g'(x)=\frac{1}{x-1}-\frac{1}{{{{(x-1)}^2}}}+2=\frac{{2x•(x-\frac{3}{2})}}{{{{(x-1)}^2}}}$,$g'(x)=0⇒x=\frac{3}{2}$,
当$x∈(1+\frac{1}{e},\frac{3}{2})$时,g'(x)<0,$x∈(\frac{3}{2},e+1)$时,g'(x)>0,
所以当$x=\frac{3}{2}$时,g(x)取得极小值6-ln2,又$g(\frac{1}{e}+1)=e+\frac{2}{e}+2$,$g(e+1)=2e+\frac{1}{e}+4$,f'(x)=0?g(x)=-b,所以
(ⅰ)当-b≤6-ln2,即b≥ln2-6时,f'(x)≥0,函数f(x)在区间$(\frac{1}{e}+1,e+1)$上无极值点;
(ⅱ)当$6-ln2<-b<e+\frac{2}{e}+2$即$-e-\frac{2}{e}-2<b<ln2-6$时,f'(x)=0有两不同解,
函数f(x)在区间$(\frac{1}{e}+1,e+1)$上有两个极值点;
(ⅲ)当$e+\frac{2}{e}+2≤-b<2e+\frac{1}{e}+4$即$-2e-\frac{1}{e}-4<b≤-e-\frac{2}{e}-2$时,f'(x)=0有一解,
函数f(x)在区间$(\frac{1}{e}+1,e+1)$上有一个极值点;
(ⅳ)当$-b≥2e+\frac{1}{e}+4$即$b≤-2e-\frac{1}{e}-4$时,f'(x)≤0,函数f(x)在区间$(\frac{1}{e}+1,e+1)$上
无极值点;
(Ⅱ)当a=1,b=e+2时,对任意的x∈(1,+∞)都有$f(x)<k•{e^{\frac{1}{2}x}}$,
即$xln(x-1)-{x^2}+(e+2)x<k{e^{\frac{x}{2}}}$,即$ln(x-1)-x+e+2<k•\frac{{{e^{\frac{x}{2}}}}}{x}$
记h(x)=ln(x-1)-x+e+2,$ϕ(x)=k•\frac{{{e^{\frac{x}{2}}}}}{x}$,
由$h'(x)=\frac{1}{x-1}-1=\frac{2-x}{x-1}$,当1<x<2时h'(x)>0,x>2时,h'(x)<0,
所以当x=2时,h(x)取得最大值h(2)=e,
又$ϕ'(x)=k\frac{{\frac{1}{2}{e^{\frac{x}{2}}}x-{e^{\frac{x}{2}}}}}{x^2}=\frac{{\frac{k}{2}{e^{\frac{x}{2}}}(x-2)}}{x^2}$,当1<x<2时ϕ'(x)<0,x>2时,ϕ'(x)>0,
所以当x=2时,ϕ(x)取得最小值$\frac{ke}{2}$,所以只需要$e<\frac{ke}{2}$⇒k>2,即正实数k的取值范围是(2,+∞).
点评 本题考查函数的导数的综合应用,函数的单调性已经函数的极值的求法,考查转化思想以及分类讨论思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1+2i | B. | 1+2i | C. | 1-2i | D. | -1-2i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
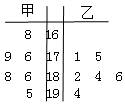 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{{16\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (-∞,-2)∪(-1,+∞) | C. | (-∞,-2) | D. | (-1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com