
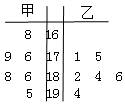
 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:分析 (1)由茎叶图先求出甲种水稻样本单株平均数,由此能估计甲种水稻的亩产.
(2)由题意知甲品种的6株中有2株超过187粒,故ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和Eξ.
解答 解:(1)由茎叶图知:
甲种水稻样本单株平均数为:
$\frac{1}{6}$(168+176+179+186+188+195)=182粒,
把样本平均数看做总体平均数,
则甲种水稻亩产约为:60000×182×$0.1×\frac{1}{1000}$=1092公斤.
(2)由题意知甲品种的6株中有2株超过187粒,故ξ的可能取值为0,1,2,
P(ξ=0)=$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{2}{5}$,
P(ξ=1)=$\frac{{C}_{2}^{1}{C}_{4}^{1}}{{C}_{6}^{2}}$=$\frac{8}{15}$,
P(ξ=2)=$\frac{{C}_{2}^{2}}{{C}_{6}^{2}}$=$\frac{1}{15}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{2}{5}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列、数学期望的求法,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
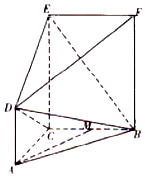 在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.
在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com