
分析 (1)关于x的不等式|x+a|≤b的解集为[-b-a,b-a],利用条件建立方程组,即可求实数a,b的值;
(2)利用|n|=$\frac{1}{9}$|(2m+n)-(2m-8n)|≤$\frac{1}{9}$|2m+n|+2|m-4n|,即可证明结论.
解答 (1)解:关于x的不等式|x+a|≤b的解集为[-b-a,b-a],
∵关于x的不等式|x+a|≤b的解集为[-6,2],
∴$\left\{\begin{array}{l}{b-a=2}\\{-b-a=-6}\end{array}\right.$,∴a=2,b=4;
(2)证明:∵实数m,n满足|am+n|<$\frac{1}{3}$,|m-bn|<$\frac{1}{6}$,
∴|n|=$\frac{1}{9}$|(2m+n)-(2m-8n)|≤$\frac{1}{9}$|2m+n|+2|m-4n|<$\frac{1}{9}(\frac{1}{3}+\frac{1}{3})$=$\frac{2}{27}$.
点评 本题考查绝对值不等式的解法,考查三角不等式的运用,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{2}{x-1}$ | B. | f(x)=lg$\frac{2}{x-1}$ | C. | f(x)=lg($\frac{2}{x}$+1) | D. | f(x)=lg(x-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
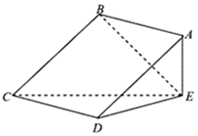 如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.
如图,正方形ABCD所在平面与三角形CDE所在平面相交于CD,AE⊥平面CDE,且AE=1,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|x<-2} | C. | {x|x<1} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={(\frac{1}{2})^x}$ | C. | y=lnx | D. | y=x2+2x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com