
分析 (1)由题意可得c=$\sqrt{2}$,把点的坐标代入椭圆方程,结合隐含条件求得a2=4,b2=2.则椭圆方程可求;
(2)设出AB所在直线方程x=ty-$\sqrt{2}$,联立直线方程和椭圆方程,由根与系数的关系得到A,B的纵坐标的和与积,求出|y1-y2|取最大值时的t值,得到A的坐标,由圆心到三边的距离相等求得最大内切圆的半径,则答案可求.
解答 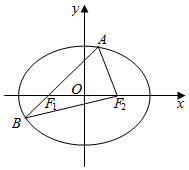 解:(1)由题意得,c=$\sqrt{2}$,
解:(1)由题意得,c=$\sqrt{2}$,
由点(-$\sqrt{2}$,1)在椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,
得$\frac{2}{{a}^{2}}+\frac{1}{{b}^{2}}=1$,①
又a2=b2+c2,∴a2=b2+2,②
联立①②解得:a2=4,b2=2.
∴椭圆方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;
(2)如图,设AB所在直线方程为x=ty-$\sqrt{2}$,
联立$\left\{\begin{array}{l}{x=ty-\sqrt{2}}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,消去x得:$({t}^{2}+2){y}^{2}-2\sqrt{2}ty-2=0$.
设A(x1,y1),B(x2,y2),
则${y}_{1}+{y}_{2}=\frac{2\sqrt{2}t}{{t}^{2}+2},{y}_{1}{y}_{2}=\frac{-2}{{t}^{2}+2}$,
$|{y}_{1}-{y}_{2}|=\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\sqrt{(\frac{2\sqrt{2}t}{{t}^{2}+2})^{2}+\frac{8}{{t}^{2}+2}}$=$4\sqrt{\frac{{t}^{2}+1}{({t}^{2}+1+1)^{2}}}$
=$4\sqrt{\frac{{t}^{2}+1}{({t}^{2}+1)^{2}+2({t}^{2}+1)+1}}$=$\sqrt{\frac{1}{({t}^{2}+1)+\frac{1}{{t}^{2}+1}+2}}$$≤\sqrt{\frac{1}{2\sqrt{({t}^{2}+1)•\frac{1}{{t}^{2}+1}}+2}}=\frac{1}{2}$.
当且仅当${t}^{2}+1=\frac{1}{{t}^{2}+1}$,即t=0时上式等号成立.
∴当AB所在直线方程为x=-$\sqrt{2}$时,△ABF2的面积最大,内切圆得半径最大,
设内切圆得圆心为(m,0),
AF2所在直线方程为$\frac{y}{1-0}=\frac{x-\sqrt{2}}{-\sqrt{2}-\sqrt{2}}$,整理得$x+2\sqrt{2}y-\sqrt{2}=0$.
由$m+\sqrt{2}=\frac{|m-\sqrt{2}|}{3}$,解得m=-$\frac{\sqrt{2}}{2}$.
∴△ABF2的内切圆的最大半径为$\frac{\sqrt{2}}{2}$,
则△ABF2的内切圆的最大周长为2π•$\frac{\sqrt{2}}{2}=\sqrt{2}π$.
点评 本题考查椭圆方程的求法,考查了椭圆的简单性质,体现了数学转化思想方法,训练了利用基本不等式求最值,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π???? | D. | 4$\sqrt{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
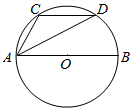 如图,AB是⊙O的直径,点C,D是半圆弧AB的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.(用a,b表示)
如图,AB是⊙O的直径,点C,D是半圆弧AB的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.(用a,b表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,1) | B. | (1,2) | ||
| C. | ($\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$)或(-$\frac{\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$) | D. | ($\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$)或(-$\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com